
科目: 来源: 题型:
【题目】几何探究:
(问题发现)
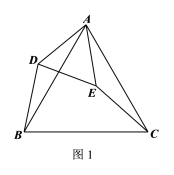
(1)如图1所示,△ABC和△ADE是有公共顶点的等边三角形,BD、CE的关系是_______(选填“相等”或“不相等”);(请直接写出答案)
(类比探究)
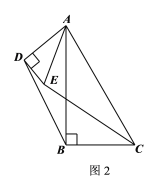
(2)如图2所示,△ABC和△ADE是有公共顶点的含有![]() 角的直角三角形,(1)中的结论还成立吗?请说明理由;
角的直角三角形,(1)中的结论还成立吗?请说明理由;
(拓展延伸)
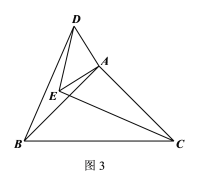
(3)如图3所示,△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形,将△ADE绕点A自由旋转,若![]() ,当B、D、E三点共线时,直接写出BD的长.
,当B、D、E三点共线时,直接写出BD的长.
查看答案和解析>>
科目: 来源: 题型:
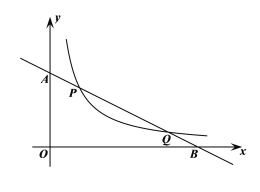
【题目】如图所示,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,与坐标轴交于A、B两点.
,与坐标轴交于A、B两点.
(1)求一次函数与反比例函数的解析式;
(2)观察图象,当![]() 时,直接写出不等式
时,直接写出不等式![]() 的解集;
的解集;
(3)将直线![]() 向下平移
向下平移![]() 个单位,若直线与反比例函数
个单位,若直线与反比例函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校拟购进一批手动喷淋消毒设备,已知1个A型喷雾器和2个B型喷雾器共需90元;2个A型喷雾器和3个B型喷雾器共需165元.
(1)问一个A型喷雾器和一个B型喷雾器的单价各是多少元?
(2)学校决定购进两种型号的喷雾器共60个,并且要求B型喷雾器的数量不能多于A型喷雾器的4倍,请你设计出最为省钱的购买方案,并说明理由.


查看答案和解析>>
科目: 来源: 题型:
【题目】2020年春季开学后,某校制定了《新冠肺炎疫情防控期间就餐规范》,条例规定:不对面就餐、食而不语、错峰就餐、鼓励打包等就餐措施.为了解学生对规范的认知程度,校园小记者随机调查部分同学,并根据调查结果绘制了如下两幅不完整的统计图表:

请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() ______;
______;
(2)求扇形统计图中B部分所对圆心角度数;
(3)学校团委及政教处准备对“不太了解”及“毫不知情”的同学进行再学习培训,请问我校2400名学生中预计有多少人要接受再学习?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,△ABC内接于⊙O,且AB为⊙O的直径,作![]() 的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.
的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.

(1)求证:△ABD为等腰直角三角形;
(2)填空:
①若![]() ,则AE的长度为_______;
,则AE的长度为_______;
②在①的条件下,延长AC、DB交于点P,则![]() ______.
______.
查看答案和解析>>
科目: 来源: 题型:
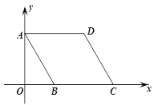
【题目】平面直角坐标系中,菱形ABCD如图所示,![]() ,点D在线段AB的垂直平分线上,若菱形ABCD绕点O逆时针旋转,旋转速度为每秒
,点D在线段AB的垂直平分线上,若菱形ABCD绕点O逆时针旋转,旋转速度为每秒![]() ,则第70秒时点D的对应坐标为( )
,则第70秒时点D的对应坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业复工之后,举行了一个简单的技工比赛,参赛的五名选手在单位时间内加工零件的合格率分别为:94.3% ,96.1% , 94.3% ,91.7% ,93.5%.关于这组数据,下列说法正确的是( )
A.平均数是93.96%B.方差是0
C.中位数是93.5%D.众数是94.3%
查看答案和解析>>
科目: 来源: 题型:
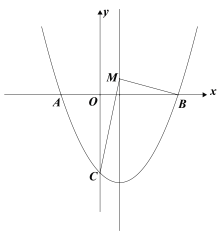
【题目】如图,抛物线y=![]() x2+mx+4m与x轴交于点A(
x2+mx+4m与x轴交于点A(![]() ,0)和点B(
,0)和点B(![]() ,0),与y轴交于点C,
,0),与y轴交于点C,![]() ,若对称轴在y轴的右侧.
,若对称轴在y轴的右侧.
(1)求抛物线的解析式
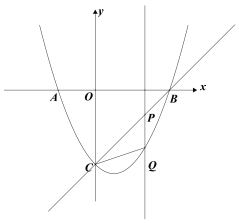
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是一条对角线,点
是一条对角线,点![]() 在直线
在直线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,平移
,平移![]() ,使点
,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
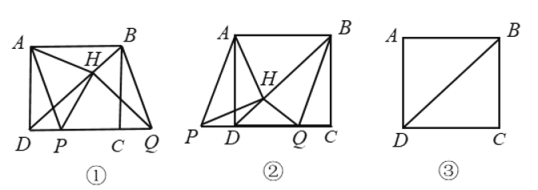
(问题发现)
(1)如图①,若点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 的数量关系是________,位置关系是________.
的数量关系是________,位置关系是________.
(拓展探究)
(2)如图②,若点![]() 在线段
在线段![]() 的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
(解决问题)
(3)若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,正方形
,正方形![]() 的边长为2,请直接写出求
的边长为2,请直接写出求![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com