
科目: 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
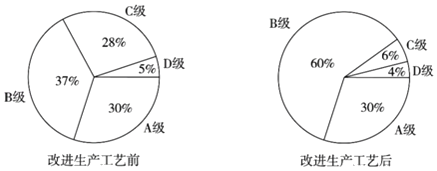
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目: 来源: 题型:
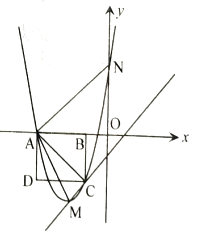
【题目】如图,边长为![]() 的正方形的边
的正方形的边![]() 在
在![]() 轴负半轴上,点
轴负半轴上,点![]() 在第三象限内,点
在第三象限内,点![]() 的坐标为
的坐标为![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 交
交![]() 轴于点
轴于点![]() ,其顶点为
,其顶点为![]() .
.
(1)求抛物线的解析式;
(2)若![]() 轴左侧抛物线上一点
轴左侧抛物线上一点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 恰好落在直线
恰好落在直线![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)连接![]() ,
,![]() ,
,![]() ,请你探究在
,请你探究在![]() 轴左侧的抛物线上,是否存在点
轴左侧的抛物线上,是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们定义:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”.
的“旋补中线”.
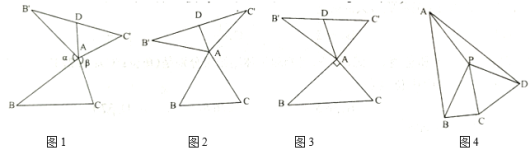
(特例感知)
(1)在图2,图3中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
①如图2,当![]() 为等边三角形,且
为等边三角形,且![]() 时,则
时,则![]() 长为 .
长为 .
②如图3,当![]() ,且
,且![]() 时,则
时,则![]() 长为 .
长为 .
(猜想论证)
(2)在图1中,当![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.(如果你没有找到证明思路,可以考虑延长
的数量关系,并给予证明.(如果你没有找到证明思路,可以考虑延长![]() 或延长
或延长![]() ,……)
,……)
(拓展应用)
(3)如图4,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为边在四边形
为边在四边形![]() 内部作等边
内部作等边![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的“旋补三角形”,请直接写出
的“旋补三角形”,请直接写出![]() 的“旋补中线”长及四边形
的“旋补中线”长及四边形![]() 的边
的边![]() 长.
长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某科技公司接到一份新型高科技产品紧急订单,要求在![]() 天内(含
天内(含![]() 天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了该种产品
天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了该种产品![]() 件,以后每天生产的产品都比前一天多
件,以后每天生产的产品都比前一天多![]() 件.由于机器损耗等原因,当日生产的产品数量达到
件.由于机器损耗等原因,当日生产的产品数量达到![]() 件后,每多生产一件,当天生产的所有产品平均每件成本就增加
件后,每多生产一件,当天生产的所有产品平均每件成本就增加![]() 元.
元.
(1)设第![]() 天生产产品
天生产产品![]() 件,求出
件,求出![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
(2)若该产品每件生产成本(日生产量不超过![]() 件时)为
件时)为![]() 元,订购价格为每件
元,订购价格为每件![]() 元,设第
元,设第![]() 天的利润为
天的利润为![]() 元,试求
元,试求![]() 与
与![]() 之间的函数解析式,并求该公司哪一天获得的利润最大,最大利润的是多少?
之间的函数解析式,并求该公司哪一天获得的利润最大,最大利润的是多少?
(3)该公司当天的利润不低于![]() 元的是哪几天?请直接写出结果.
元的是哪几天?请直接写出结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解停课不停学,期间,同学们居家学习的情况,某校从全校学生中随机抽取部分学生进行网络问卷调查,并将调查结果分成(![]() :优,
:优,![]() :良,
:良,![]() :中,
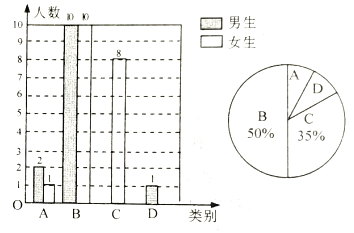
:中,![]() :差)四类.依据调查结果绘制成两幅不完整的统计图
:差)四类.依据调查结果绘制成两幅不完整的统计图
(1)这次被调查的学生一共有 人,其中![]() (中)等次的男生有 人,表示
(中)等次的男生有 人,表示![]() (差)等次的扇形所对的圆心角的度数为 度;
(差)等次的扇形所对的圆心角的度数为 度;
(2)若该校约有![]() 名学生,估计全校居家学习处于优或良(
名学生,估计全校居家学习处于优或良(![]() 或
或![]() )等次的学生有多少人?
)等次的学生有多少人?
(3)为了共同进步,刘老师想从被调查的![]() 类和
类和![]() 类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
查看答案和解析>>
科目: 来源: 题型:
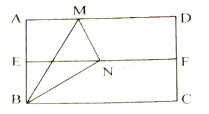
【题目】如图,在矩形纸片![]() 中,
中,![]() ,对折矩形纸片
,对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,展平后再过点
,展平后再过点![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕为
,折痕为![]() .再次展平,连接
.再次展平,连接![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() 与
与![]() 相似;③
相似;③![]() 的长为
的长为![]() :④若
:④若![]() 分别为线段
分别为线段![]() 上的动点(不包含端点),则
上的动点(不包含端点),则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目: 来源: 题型:
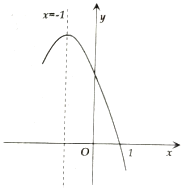
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,其部分图象如图所示对于此抛物线有如下四个结论:①
,其部分图象如图所示对于此抛物线有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 若,则
若,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值其中正确结论的个数是( )
时的函数值其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com