
科目: 来源: 题型:
【题目】“特色江苏,美好生活”,第十届江苏省园艺博览会在扬州举行.圆圆和满满同学分析网上关于园博会的信息,发现最具特色的场馆有:扬州园,苏州园,盐城园,无锡园.他们准备周日下午去参观游览,各自在这四个园中任选一个,每个园被选中的可能性相同.
(1)圆圆同学在四个备选园中选中扬州园的概率是 .
(2)用树状图或列表法求出圆圆和满满他们选中同一个园参观的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分8分) 青少年沉迷于手机游戏,严重危害他们的身心健康,此问题已引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的“王者荣耀”玩家进行了简单的随机抽样调查,绘制出以下两幅统计图.
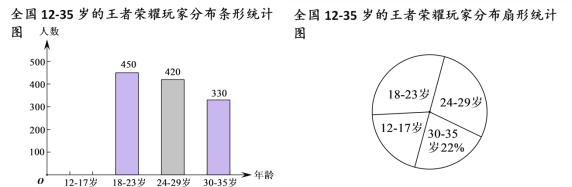
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是_________;
(3)据报道,目前我国12﹣35岁“王者荣耀”玩家的人数约为2000万,请估计其中12﹣23岁的人数.
(4)根据对统计图表的分析,请你为沉迷游戏的同学提一个合理化建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
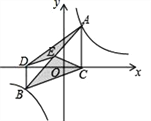
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
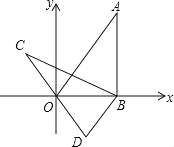
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P在直线AB上方,且满足S△PABS:矩形ABCD=1:3,则使△PAB为直角三角形的点P有( )个
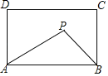
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(3,0),在第一象限内与直线y=x交于点B(4,t).
(1)求这条抛物线的表达式;
(2)在直线OB下方的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积最大,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=-![]() x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)当正方形PQMN的边MN经过点B时,t= 秒;
(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)连结BN,则BN的最小值为 .
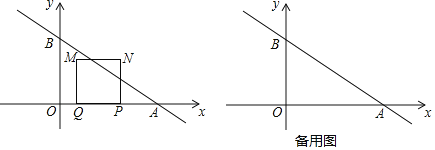
查看答案和解析>>
科目: 来源: 题型:
【题目】问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
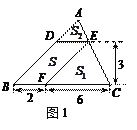
四边形DBFE的面积![]() ,
,
△EFC的面积![]() ,
,
△ADE的面积![]() .
.
探究发现
(2)在(1)中,若![]() ,
,![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.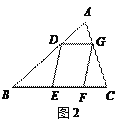
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且∠DAE=∠FAE.
(1)求证:AD为⊙O切线;
(2)若sin∠BAC=![]() ,求tan∠AFO的值.
,求tan∠AFO的值.
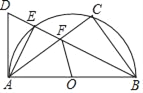
查看答案和解析>>
科目: 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com