
科目: 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
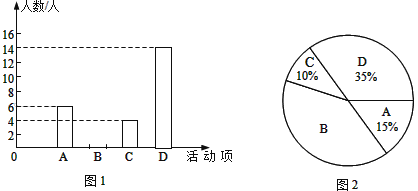
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于A(2,﹣1)、B(
(x>0)的图象交于A(2,﹣1)、B(![]() ,n)两点.直线y=2与y轴交于点C.
,n)两点.直线y=2与y轴交于点C.
1)求一次函数与反比例函数的解析式;
2)求△ABC的面积;
3)直接写出不等式kx+b>![]() 在如图所示范围内的解集.
在如图所示范围内的解集.

查看答案和解析>>
科目: 来源: 题型:
【题目】小红乘坐小船往返于A、B两地,其中从A地到B地是顺流行驶.当小红第一次从A地出发时,小明同时乘坐橡皮艇从A、B之间的C地漂流而下,直至到达B地.已知A地分别距离B、C两地20千米和8千米,小船顺流速度为20千米/时,逆流速度为10千米/时,则小红、小明在途中相遇时距离C地_____千米.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示是二次函数y=ax2+bx+c的图象.下列结论:①二次三项式ax2+bx+c的最大值为4;②使y≤3成立的x的取值范围是x≤-2;③一元二次方程ax2+bx+c=1的两根之和为-1;④该抛物线的对称轴是直线x=-1;⑤4a-2b+c<0.其中正确的结论有______________.(把所有正确结论的序号都填在横线上)
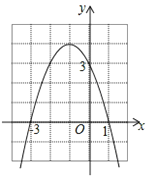
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y1=kx2+ax+a的图象与x轴交于点A,B(点A在点B的左侧),函数y2=kx2+bx+b,的图象与x轴交于点C,D(点C在点D的左侧),其中k≠0,a≠b.
(1)求证:函数y1与y2的图象交点落在一条定直线上;
(2)若AB=CD,求a,b和k应满足的关系式;
(3)是否存在函数y1和y2,使得B,C为线段AD的三等分点?若存在,求![]() 的值,若不存在,说明理由
的值,若不存在,说明理由
查看答案和解析>>
科目: 来源: 题型:
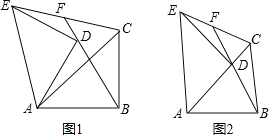
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转,得到△ADE,旋转角为α(0°<α<90°),连接BD交CE于点F.
(1)如图2,当α=45°时,求证:CF=EF;
(2)在旋转过程中,①问(1)中的结论是否仍然成立?证明你的结论;②连接CD,当△CDF为等腰直角三角形时,求tan![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
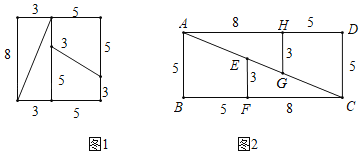
【题目】直觉的误差:有一张8cm×8cm的正方形纸片,面积是64cm2.把这些纸片按图1所示剪开成四小块,其中两块是三角形,另外两块是梯形.把剪出的4个小块按图2所示重新拼合,这样就得到了一个13cm×5cm的长方形,面积是65cm2,面积多了1cm2,这是为什么?
小明给出如下证明:如图2,可知,tan∠CEF=![]() ,tan∠EAB=
,tan∠EAB=![]() ,∵tan∠CEF>tan∠EAB,∴∠CEF>∠EAB,∵EF∥AB,∴∠EAB+∠AEF=180°,∴CEF+∠AEF>180°,因此A、E、C三点不共线.同理A、G、C三点不共线,所以拼合的长方形内部有空隙,故面积多了1cm2
,∵tan∠CEF>tan∠EAB,∴∠CEF>∠EAB,∵EF∥AB,∴∠EAB+∠AEF=180°,∴CEF+∠AEF>180°,因此A、E、C三点不共线.同理A、G、C三点不共线,所以拼合的长方形内部有空隙,故面积多了1cm2
(1)小红给出的证明思路为:以B为原点,BC所在的直线为x轴,建立平面直角坐标系,证明三点不共线.请你帮小红完成她的证明;
(2)将13cmx13cm的正方形按上述方法剪开拼合,是否可以拼合成一个长方形,但面积少了1cm2?如果能,求出剪开的三角形的短边长;如果不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市“木兰溪左岸绿道”工程已全部建成并投入使用,10公里的河堤便道铺满了彩色的透水沥青,堤岸旁的各类花草争奇斗艳,与木兰溪河滩上的特色花草相映成趣,吸引着众多市民在此休闲锻炼、散步观光.某小区随机调查了部分居民在一周内前往“木兰溪左岸绿道”锻炼的次数,并制成如图不完整的统计图表:
居民前往“木兰溪左岸绿道”锻炼的次数统计表
锻炼次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= .
(2)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(3)若该小区共有2000名居民,根据调查结果,估计该小区居民在一周内前往木兰溪左岸绿道”锻炼“4次及以上”的人数.

查看答案和解析>>
科目: 来源: 题型:
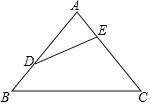
【题目】如图,△ABC中,AB=AC,∠A=80°,点D,E分别在边AB,AC上,且DA=DE=CE.
(1)求作点F,使得四边形BDEF为平行四边形;(要求:尺规作图,保留痕迹,不写作法)
(2)连接CF,写出图中经过旋转可完全重合的两个三角形,并指出旋转中心和旋转角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com