
科目: 来源: 题型:
【题目】如图,直线y1=2x+2交x轴、y轴于点A、C,直线![]() 交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
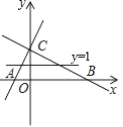
A.2B.2.5C.3D.3.5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论中正确的有( )
①4ac<b2
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③3a+c>0
④当y>0时,取值范围是﹣1≤x≤3
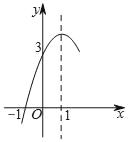
A. ①②B. ①②③C. ①③④D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a、b、c为正数,若关于x的一元二次方程ax2+bx+c=0有两个实数根,则关于x的方程a2x2+b2x+c2=0解的情况为( )
A.有两个不相等的正根B.有一个正根,一个负根
C.有两个不相等的负根D.不一定有实数根
查看答案和解析>>
科目: 来源: 题型:
【题目】在直线l上摆放着三个正方形
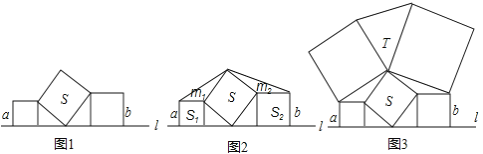
(1)如图1,已知水平放置的两个正方形的边长依次是a,b斜着放置的正方形的面积S= ,两个直角三角形的面积和为 ;(均用a,b表示)
(2)如图2,小正方形面积S1=1,斜着放置的正方形的面积S=4,求图中两个钝角三角形的面积m1和m2,并给出图中四个三角形的面积关系;
(3)图3是由五个正方形所搭成的平面图,T与S分别表示所在的三角形与正方形的面积,试写出T与S的关系式,并利用(1)和(2)的结论说明理由.
查看答案和解析>>
科目: 来源: 题型:
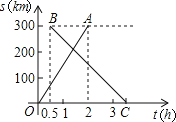
【题目】宁波与台州两城市之间开通了动车组高速列车.已知每隔1h有一列速度相同的动车组列车从宁波开往台州.如图所示,OA是第一列动车组列车离开宁波的路程s(单位:km)与运行时间t(单位:h)的函数图象,BC是一列从台州开往宁波的普通快车距宁波的路程s(单位:km)与运行时间t(单位:h)的函数图象.请根据图中信息,解答下列问题:
(1)点B横坐标0.5的意义是普通快车的发车时间比第一列动车组列车的发车时间晚 h,点B的纵坐标300的意义是 ;
(2)若普通列车的速度为100km/h,
①求BC的解析式;
②求第二列动车组列车出发后多长时间与普通列车相遇.
查看答案和解析>>
科目: 来源: 题型:
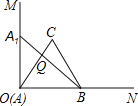
【题目】已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A于点O重合,顶点C在∠MON内部
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法);
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1,试猜想∠BCC1为多少度,并证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国农村劳动力人数有4.8亿.从目前来看,我国农民的科技水平还不高,在农村4.8亿的劳动力中,小学文化程度以下的占40%,具有初中文化程度的占48%,具有高中文化程度的占12%,受过职业技术培训的占5%,但据专家统计,他们中八成以上会进行分数、平均数、增长率等基本数学运算,能基本适应当代经济生活,这是初等数学教育的一大成就.
请根据上面的数据信息解答下列问题:
文化程度 | 人数(亿) | 会基本数学运算人数(亿) | 百分比 |
小学以下 | 1.4976 | ||
初中文化 | 2.0736 | 90% | |
高中文化 | 95% | ||
受过职业技术培训 | 0.2328 | 97% |
(1)填写下列农民受教育情况及掌握基本数学运算情况统计
(2)根据图表,求出农村劳动力中会进行基本数学运算的总人数占农村劳动力总人数的百分比;
(3)政府计划两年后使农村劳动力初、高中文化程度达到80%,那么平均每年增长的百分率是多少(精确到0.1%)?
查看答案和解析>>
科目: 来源: 题型:
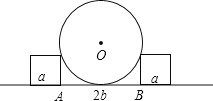
【题目】在汽车车轮修理厂,工人师傅常用两个棱长为a的正方形卡住车轮.如图是其截面图(a小于车轮半径),量出两个正方形的距离AB的长为2b,就可以得出车轮的直径.请你推求出直径d的公式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC边在x轴正半轴上,中线BD的反向延长线交y轴负半轴于点E.双曲线y=![]() 一条分支经过点A,若S△BEC=4,则k等于( )
一条分支经过点A,若S△BEC=4,则k等于( )
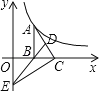
A. 4B. 8C. 12D. 16
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com