
科目: 来源: 题型:
【题目】如图所示,O为△ABC内一点.
(1)以O为位似中心,作△A1B1C1,使△A1B1C1与△ABC的相似比为2∶1;
(2)以O为位似中心,作△A2B2C2,使△A2B2C2与△ABC的相似比为1∶2;
(3)若△ABC的周长为12 cm,面积为6cm2,请分别求出△A1B1C1,△A2B2C2的周长和面积.

查看答案和解析>>
科目: 来源: 题型:
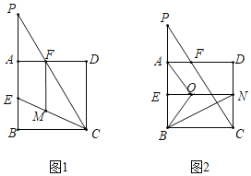
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 延长线上的一点,连接
延长线上的一点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)如图1,连接![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图2,过点![]() 作
作![]() 于点
于点![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .将
.将![]() 绕点
绕点![]() 旋转,使点
旋转,使点![]() 旋转后的对应点
旋转后的对应点![]() 落在边
落在边![]() 上.请判断点
上.请判断点![]() 旋转后的对应点
旋转后的对应点![]() 是否落在线段
是否落在线段![]() 上,并说明理由.
上,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为常数)的图象经过点
为常数)的图象经过点![]() .
.
(1)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)设该函数图象的顶点坐标是![]() ,当
,当![]() 的值变化时,求
的值变化时,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)若该函数的图象不经过第三象限,当![]() 时,函数的最大值与最小值之差为16,求
时,函数的最大值与最小值之差为16,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.

(1)已知凸五边形![]() 的各条边都相等.
的各条边都相等.
①如图1,若![]() ,求证:五边形
,求证:五边形![]() 是正五边形;
是正五边形;
②如图2,若![]() ,请判断五边形
,请判断五边形![]() 是不是正五边形,并说明理由:
是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形![]() 的各条边都相等.
的各条边都相等.
①若![]() ,则六边形
,则六边形![]() 是正六边形;( )
是正六边形;( )
②若![]() ,则六边形
,则六边形![]() 是正六边形. ( )
是正六边形. ( )
查看答案和解析>>
科目: 来源: 题型:
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.
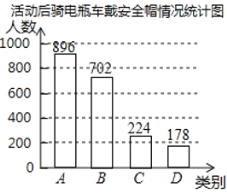

活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
查看答案和解析>>
科目: 来源: 题型:
【题目】砸“金蛋”游戏:把210个“金蛋”连续编号为1,2,3,…,210,接着把编号是3的整数倍的“金蛋”全部砸碎;然后将剩下的“金蛋”重新连续编号为1,2,3,…,接着把编号是3的整数倍的“金蛋”全部砸碎……按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止.操作过程中砸碎编号是“66”的“金蛋”共_____个.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已如抛物线y=-x2+3x+m,其中m为常数
(I)当抛物线经过点(3,5)时,求该抛物线的解析式。
(II)当抛物线与直线y=x+3m只有一个交点时,求该抛物线的解析式。
(III)当0≤x≤4时,试通过m的取值范围讨论抛物线与直线y=x+2的公共点的个数的情况
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,矩形![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上。
上。
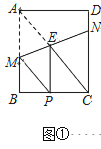

Ⅰ.如图①,当![]() 时,①求证
时,①求证![]() ;②求
;②求![]() 的长;
的长;
Ⅱ.请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长。
的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售;方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。
设公司一次性购买此型号笔记本电脑![]() 台。
台。
Ⅰ.根据题意,填写下表:
购买台数 | 3 | 10 | 20 | … |
方案一的总费用(元) | 13500 | 45000 | 90000 | … |
方案二的总费用(元) | 15000 | … |
Ⅱ.设选择方案一的费用为![]() 元,选择方案二的费用为
元,选择方案二的费用为![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
Ⅲ.当![]() 时,该公司采用哪种方案购买更合算?并说明理由。
时,该公司采用哪种方案购买更合算?并说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁,
(I)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 .
(II)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com