
科目: 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,AD是
,AD是![]() 的角平分线,且
的角平分线,且![]() ,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
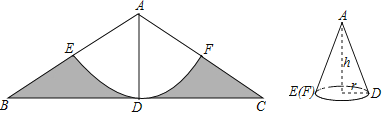
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 平分
平分![]() ,交弦
,交弦![]() 于点
于点![]() ,连接半径
,连接半径![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的一条直线交
的一条直线交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
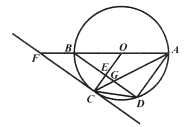
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)若![]() .
.
①求![]() 的长;
的长;
②求![]() 的周长.(结果可保留根号)
的周长.(结果可保留根号)
查看答案和解析>>
科目: 来源: 题型:
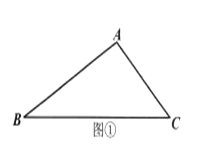
【题目】按要求解答下列各题:
(1)如图①,求作一点![]() ,使点
,使点![]() 到
到![]() 的两边的距离相等,且在
的两边的距离相等,且在![]() 的边
的边![]() 上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);
上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);
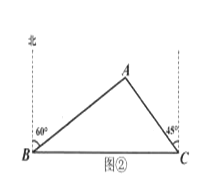
(2)如图②,![]() 表示两个港口,港口
表示两个港口,港口![]() 在港口
在港口![]() 的正东方向上.海上有一小岛
的正东方向上.海上有一小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 方向上,且在港口
方向上,且在港口![]() 的北偏西
的北偏西![]() 方向上.测得
方向上.测得![]() 海里,求小岛
海里,求小岛![]() 与港口
与港口![]() 之间的距离.(结果可保留根号)
之间的距离.(结果可保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明为了了解本校学生的假期活动方式,随机对本校的部分学生进行了调查.收集整理数据后,小明将假期活动方式分为五类:A.读书看报;B.健身活动;C.做家务;D.外出游玩;E.其他方式,并绘制了不完整的统计图如图.统计后发现“做家务”的学生人数占调查总人数的![]() .
.
请根据图中的信息解答下列问题:
(1)本次调查的总人数是 人;
(2)补全条形统计图;
(3)根据调查结果,估计本校![]() 名学生中“假期活动方式”是“读书看报”的有多少人?
名学生中“假期活动方式”是“读书看报”的有多少人?
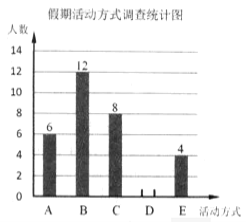
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]()
(1)请在网格中,画出线段![]() 关于原点对称的线段
关于原点对称的线段![]() ;
;
(2)请在网格中,过点![]() 画一条直线
画一条直线![]() ,将
,将![]() 分成面积相等的两部分,与线段
分成面积相等的两部分,与线段![]() 相交于点
相交于点![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(3)若另有一点![]() ,连接
,连接![]() ,则
,则![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两台机器共同加工一批零件,一共用了![]() 小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数
小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数![]() (个)与甲加工时间
(个)与甲加工时间![]() 之间的函数图象为折线
之间的函数图象为折线![]() ,如图所示.
,如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?
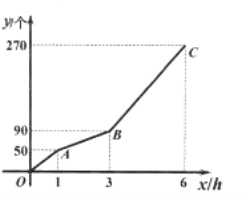
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的两个动点,
上的两个动点,![]() 是正方形四边上的任意一点,且
是正方形四边上的任意一点,且![]() ,设
,设![]() .当
.当![]() 是等腰三角形时,下列关于
是等腰三角形时,下列关于![]() 点个数的说法中,一定正确的是( )
点个数的说法中,一定正确的是( )
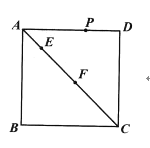
①当![]() (即
(即![]() 两点重合)时,
两点重合)时,![]() 点有
点有![]() 个
个
②当![]() 时,
时,![]() 点最多有
点最多有![]() 个
个
③当![]() 点有
点有![]() 个时,x=2
个时,x=2![]() ﹣2
﹣2
④当![]() 是等边三角形时,
是等边三角形时,![]() 点有4个
点有4个
A. ①③B. ①④C. ②④D. ②③
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中有抛物线y=a(x﹣2)2﹣2和y=a(x﹣h)2,抛物线y=a(x﹣2)2﹣2经过原点,与x轴正半轴交于点A,与其对称轴交于点B;点P是抛物线y=a(x﹣2)2﹣2上一动点,且点P在x轴下方,过点P作x轴的垂线交抛物线y=a(x﹣h)2于点D,过点D作PD的垂线交抛物线y=a(x﹣h)2于点D′(不与点D重合),连接PD′,设点P的横坐标为m:
(1)①直接写出a的值;
②直接写出抛物线y=a(x﹣2)2﹣2的函数表达式的一般式;
(2)当抛物线y=a(x﹣h)2经过原点时,设△PDD′与△OAB重叠部分图形周长为L:
①求![]() 的值;
的值;
②直接写出L与m之间的函数关系式;
(3)当h为何值时,存在点P,使以点O、A、D、D′为顶点的四边形是菱形?直接写出h的值.
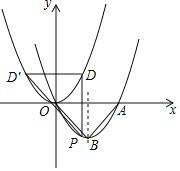
查看答案和解析>>
科目: 来源: 题型:
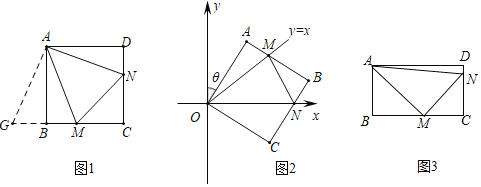
【题目】(1)问题背景:
如图1,在正方形ABCD中,点M,N分别在边BC,CD上,连接MN,且∠MAN=45°,将△ADN绕点A顺时针旋转90°,得到△ABG,可证△AMG≌△AMN,易得线段MN、BM、DN之间的数量关系为: (直接填写);
(2)实践应用:
在平面直角坐标系中,边长为5的正方形OABC的两顶点分别在y轴、x轴的正半轴上,O在原点.现将正方形OABC绕点O按顺时针方向旋转,旋转角为θ,当点A第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.如图2,设△MBN的周长为P,在旋转正方形OABC的过程中,P值是否有变化?请证明你的结论;
(3)拓展研究:
如图3,将正方形改为长与宽不相等的矩形,且∠MAN=∠CMN=45°,请你直接写出线段MN、BM、DN之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com