
科目: 来源: 题型:
【题目】已知函数 (
(![]() 为常数)
为常数)
(1)当![]() ,
,
①点![]() 在此函数图象上,求
在此函数图象上,求![]() 的值;
的值;
②求此函数的最大值.
(2)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,当此函数的图象与线段
,当此函数的图象与线段![]() 只有一个交点时,直接写出
只有一个交点时,直接写出![]() 的取值范围.
的取值范围.
(3)当此函数图象上有4个点到![]() 轴的距离等于4,求
轴的距离等于4,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
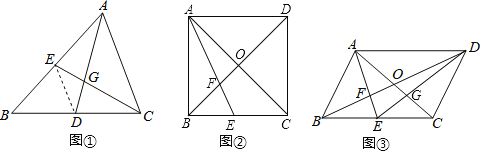
【题目】教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 相交于点
相交于点![]() ,求证:
,求证:![]() ,
,
证明:连结![]() .
.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图②,若![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 的长为 .
的长为 .
(2)如图③,连结![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 .
的面积为 .
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止.甲、乙两车相距的路程
地,两车分别到达目的地后停止.甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示.
(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时,![]() ,
,![]() .
.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)当甲车到达距![]() 地70千米处时,求甲、乙两车之间的路程.
地70千米处时,求甲、乙两车之间的路程.

查看答案和解析>>
科目: 来源: 题型:
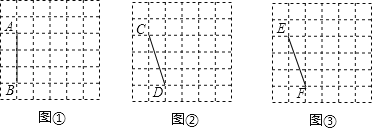
【题目】图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点![]() 均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以线段![]() 为边画一个
为边画一个![]() ,使其面积为6.
,使其面积为6.
(2)在图②中以线段![]() 为边画一个
为边画一个![]() ,使其面积为6.
,使其面积为6.
(3)在图③中以线段![]() 为边画一个四边形
为边画一个四边形![]() ,使其面积为9,且
,使其面积为9,且![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】网上学习越来越受到学生的喜爱.某校信息小组为了解七年级学生网上学习的情况,从该校七年级随机抽取20名学生,进行了每周网上学习的调查.数据如下(单位:时):
3 | 2.5 | 0.6 | 1.5 | 1 | 2 | 2 | 3.3 | 2.5 | 1.8 |
2.5 | 2.2 | 3.5 | 4 | 1.5 | 2.5 | 3.1 | 2.8 | 3.3 | 2.4 |
整理上面的数据,得到表格如下:
网上学习时间 |
|
|
|
|
人数 | 2 | 5 | 8 | 5 |
样本数据的平均数、中位数、众数如下表所示:
统计量 | 平均数 | 中位数 | 众数 |
数值 | 2.4 |
|
|
根据以上信息,解答下列问题:
(1)上表中的中位数![]() 的值为 ,众数
的值为 ,众数![]() 的值为 .
的值为 .
(2)用样本中的平均数估计该校七年级学生平均每人一学期(按18周计算)网上学习的时间.
(3)已知该校七年级学生有200名,估计每周网上学习时间超过2小时的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校对某班学生“五·一”小长假期间的度假情况进行调查,并根据收集的数据绘制了两幅不完整的统计图,请你根据图中提供的信息解答下面的问题:
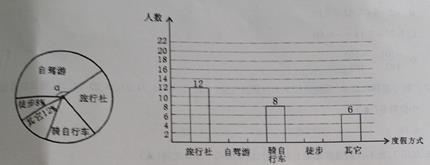
(1)求出该班学生的总人数.
(2)补全频数分布直方图.
(3)求出扇形统计图中∠α的度数.
(4)你更喜欢哪一种度假方式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于半圆,AB为直径,过点A作直线MN,若∠MAC=∠ABC.

(1)求证:MN是半圆的切线.
(2)设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F,求证:FD=FG.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
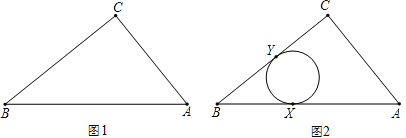
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com