
科目: 来源: 题型:
【题目】今年是中华人民共和国建国70周年,襄阳市某学校开展了“我和我的祖国”主题学习竞赛活动.学校3000名学生全部参加了竞赛,结果所有学生成绩都不低于60分(满分100分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表.根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
| 15 | 0.30 |
|
| 0.40 |
| 10 |
|
| 5 | 0.10 |
(1)表中![]() ,
,![]() ;
;
(2)这组数据的中位数落在 范围内;
(3)判断:这组数据的众数一定落在![]() 范围内,这个说法 (填“正确”或“错误”);
范围内,这个说法 (填“正确”或“错误”);
(4)这组数据用扇形统计图表示,成绩在![]() 范围内的扇形圆心角的大小为 ;
范围内的扇形圆心角的大小为 ;
(5)若成绩不小于80分为优秀,则全校大约有 名学生获得优秀成绩.
查看答案和解析>>
科目: 来源: 题型:
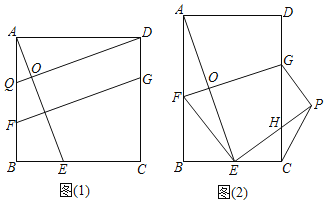
【题目】(1)证明推断:如图(1),在正方形![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() 于点
于点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() .
.
①求证:![]() ;
;
②推断:![]() 的值为 ;
的值为 ;
(2)类比探究:如图(2),在矩形![]() 中,
中,![]() (
(![]() 为常数).将矩形
为常数).将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .试探究
.试探究![]() 与
与![]() CP之间的数量关系,并说明理由;
CP之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接![]() ,当
,当![]() 时,若
时,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
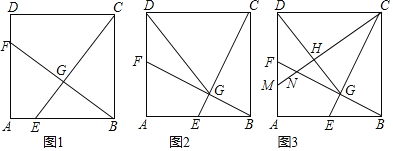
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,当点![]() 运动到
运动到![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,分别交
,分别交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛,需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具.已知毎袋贴纸有50张,毎袋小红旗有20面,贴纸和小红旗需整袋购买,每袋贴纸价格比每袋小红旗价格少5元,用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.
(1)求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果给每位演出学生分发国旗图案贴纸2张,小红旗1面.设购买国旗图案贴纸![]() 袋(
袋(![]() 为正整数),则购买小红旗多少袋能恰好配套?请用含
为正整数),则购买小红旗多少袋能恰好配套?请用含![]() 的代数式表示.
的代数式表示.
(3)在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
查看答案和解析>>
科目: 来源: 题型:
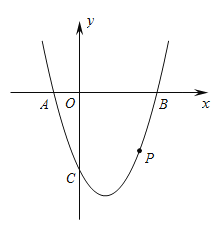
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .
.![]() 为抛物线上一点,横坐标为
为抛物线上一点,横坐标为![]() ,且
,且![]() .
.
⑴求此抛物线的解析式;
⑵当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值;
面积的最大值;
⑶设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .
.
①求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,直接写出
时,直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
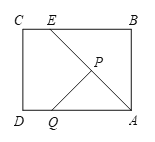
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() ,连接
,连接![]() .动点
.动点![]() 从点
从点![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度沿
的速度沿![]() 向终点
向终点![]() 运动;点
运动;点![]() 以
以![]() 的速度沿折线
的速度沿折线![]() 向终点
向终点![]() 运动.设点
运动.设点![]() 运动的时间为
运动的时间为![]() ,在运动过程中,点
,在运动过程中,点![]() ,点
,点![]() 经过的路线与线段
经过的路线与线段![]() 围成的图形面积为
围成的图形面积为![]() .
.
⑴![]() ________
________![]() ,
,![]() ________°;
________°;
⑵求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
⑶当![]() 时,直接写出
时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】性质探究
如图①,在等腰三角形![]() 中,
中,![]() ,则底边
,则底边![]() 与腰
与腰![]() 的长度之比为________.
的长度之比为________.
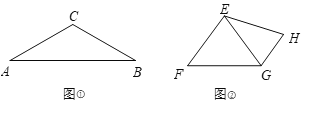
理解运用
⑴若顶角为120°的等腰三角形的周长为![]() ,则它的面积为________;
,则它的面积为________;
⑵如图②,在四边形![]() 中,
中,![]() .
.
①求证:![]() ;
;
②在边![]() 上分别取中点
上分别取中点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
类比拓展
顶角为![]() 的等腰三角形的底边与一腰的长度之比为________(用含
的等腰三角形的底边与一腰的长度之比为________(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com