
科目: 来源: 题型:
【题目】若直线l : y kx b k 0 与曲线有 n 个交点,则称直线l 为曲线的“ n 阶共生直线”,交点称为它们的“共生点”.
(1)若直线 y kx b k 0与某曲线的一个“共生点”为 P m, 2m 1,试判断此“共生点”不可能位于第几象限,请说明理由.
(2)若直线 l : y kx 2k k 0 与 x 、 y 轴分别交于 A 、 B 两点,且直线 l 为反比例函数y=![]() 的“ 2阶共生直线”,且“共生点”为C、D
的“ 2阶共生直线”,且“共生点”为C、D![]() ,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
(3)若直线l : y kx 2k k 0 与 x 轴交于点 A ,且直线l 为抛物线 y x2 2x 1的“2 阶共生直线”,且“共生点”为 P 、Q xP xQ ,若 AQ 3AP ,求 k 的值.
查看答案和解析>>
科目: 来源: 题型:
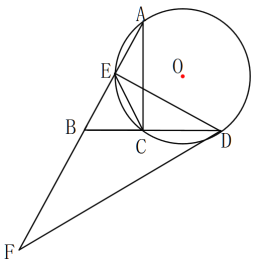
【题目】如图,在 RtABC 中,ACB 90 ,点 E 为 AB 中点,经过 A 、C 、E 三点的⊙O 与 BC的延长线相交于点 D ,过点 D 的直线交 AB 的延长线于点 F ,且FDB CED 。
(1)求证: DF 为⊙O 的切线;
(2)若 AE ![]() ,CD 1,求 DF ;
,CD 1,求 DF ;
(3)若 BF mBE ,求sin BAC (用含 m 的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】在紧张的中考复习之际,为确保学生的饮食健康与安全,部分家长组织成立中考护卫小分队,每天不辞辛劳从城区进购正规检疫菜品。某甲、乙两种菜品每份进价分别为 14 元、16 元,售价均为每份 18 元,这两种菜品每天的进价总额为 1480 元,全部销售完每天总利润为 320 元.
(1)该甲、乙两种菜品每天各卖出多少份?
(2)因受气温变化的影响,甲种菜品进价每份上涨 a 0 a 4元,为确保学生的营养,在每天两种菜品的进购总量不变的情况下,要求甲种菜品的数量不得低于 10 份,也不超过乙种菜品的 3 倍,则进购甲种菜品多少份才能使每天的总利润最大.
查看答案和解析>>
科目: 来源: 题型:
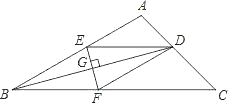
【题目】如图,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分别交 AB, BC, BD于 E, F , G ,连接 DE, DF 。
(1)求证:四边形 BEDF 为菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接市教育局开展的“创先争优”主题演讲活动,某校组织党员教师进行演讲预赛.学校将所有参赛教师的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:
组别 | 成绩x | 组中值 | 频数 |
第一组 | 90≤x≤100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | |
第三组 | 70≤x<80 | 75 | 8 |
第四组 | 60≤x<70 | 65 |
观察图表信息,回答下列问题:
(1)参赛教师共有 人;
(2)如果将各组的组中值视为该组的平均成绩,请你估算所有参赛教师的平均成绩;
(3)成绩落在第一组的恰好是两男两女四位教师,学校从中随机挑选两位教师参加市教育局组织的决赛.通过列表或画树状图求出挑选的两位教师是一男一女的概率.
查看答案和解析>>
科目: 来源: 题型:
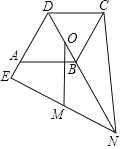
【题目】已知菱形 ABCD 中, ADC 120 , F 为 DB 延长线上一点, E 为 DA 延长线上一点, 且 BF DE , 连 CF 、 EF , 点 O 为 BD 的中点, 过 O 作 OM AB 交 EF 于 M , 若OM ![]() ,AE 1,则 AB 的长度为( )
,AE 1,则 AB 的长度为( )
A.![]() B.2C.
B.2C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() .
.
(1)若该抛物线与x轴有公共点,求c的取值范围;
(Ⅱ)设该抛物线与直线![]() 交于M,N两点,若
交于M,N两点,若![]() ,求C的值;
,求C的值;
(Ⅲ)点P,点Q是抛物线上位于第一象限的不同两点,![]() 都垂直于x轴,垂足分别为A,B,若
都垂直于x轴,垂足分别为A,B,若![]() ,求c的取值范围.
,求c的取值范围.
查看答案和解析>>
科目: 来源: 题型:
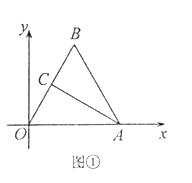
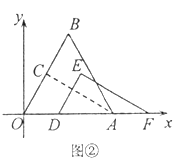
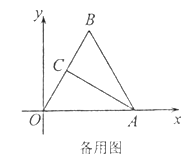
【题目】在平面直角坐标系中,点A(4,0),B为第一象限内一点,且![]() 为等边三角形,C为OB的中点,连接AC.
为等边三角形,C为OB的中点,连接AC.
(I)如图①,求点C的坐标;
(I)如图②,将![]() 沿x轴向右平移得到
沿x轴向右平移得到![]() ,设
,设![]() ,其中
,其中![]()
①设![]() 与
与![]() 重叠部分的面积为S,用含m的式子表示S:
重叠部分的面积为S,用含m的式子表示S:
②连接![]() ,当
,当![]() 取最小值时,求点E的坐标(直接写出结果即可).
取最小值时,求点E的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com