科目： 来源： 题型：
【题目】如图，在ABCD中，点P是AB边上一点
不与A，B重合
，
，过点作
，交AD边于点Q，连结CQ．
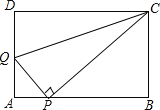
若
，求证：四边形ABCD是矩形；
在的条件下，当
，
时，求AQ的长．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE的长为（ ）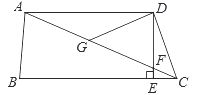
A. 
B. 
C. 
D. 
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在△ABC中，AB=AC=10cm，BC=16cm，DE=4cm．动线段DE（端点D从点B开始）沿BC边以1cm/s的速度向点C运动，当端点E到达点C时运动停止．过点E作EF∥AC交AB于点F（当点E与点C重合时，EF与CA重合），连接DF，设运动的时间为t秒（t≥0）．
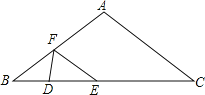
（1）直接写出用含t的代数式表示线段BE、EF的长；
（2）在这个运动过程中，△DEF能否为等腰三角形？若能，请求出t的值；若不能，请说明理由；
（3）设M、N分别是DF、EF的中点，求整个运动过程中，MN所扫过的面积．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
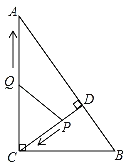
（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）是否存在某一时刻，使得PQ分△ACD的面积为2：3？若存在，求出t的值，若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图①，窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法，褶皱之后的窗帘更能彰显其飘逸、灵动的效果．其中，窗宽度的1.5倍为平褶皱，窗宽度的2倍为波浪褶皱．如图②，小莉房间的窗户呈长方形，窗户的宽度（AD）比高度（AB）的少0.5m，某种窗帘的价格为120元/m2．如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元，求小莉房间窗户的宽度与高度．
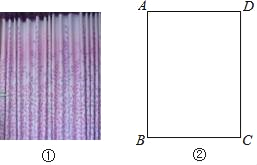
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，已知△PAB的三个顶点落在格点上．（注：每个小正方形的边长均为1）．
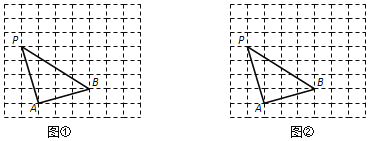
（1）△PAB的面积为 ；
（2）在图①中，仅用直尺画出一个以A为位似中心，与△PAB相似比为1：2的三角形；
（3）在图①中，画一个以AB为边且面积为6的格点三角形ABC，符合条件的点C共 个；
（4）在图②中，只借助无刻度的直尺，在图中画出一个以AB为一边且面积为12的矩形ABMN．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，四边形 ACDE 是证明勾股定理时用到的一个图形，a 、b 、c 是 RtABC和 RtBED 的边长，已知
，这时我们把关于 x 的形如
二次方程称为“勾系一元二次方程”．
请解决下列问题：
(1)写出一个“勾系一元二次方程”；
(2)求证：关于 x 的“勾系一元二次方程”，必有实数根；
(3)若 x 1是“勾系一元二次方程” 的一个根，且四边形 ACDE 的周长是6
，求ABC 的面积．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P，且AE=CF.
(1)求证：AF=BE，并求∠FPB的度数；
(2)若AE=2，试求AP·AF的值．
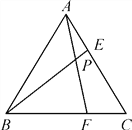
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
