
科目: 来源: 题型:
【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
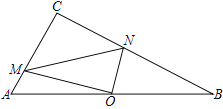
【题目】在Rt△ABC中,∠C=90°,点O是AB的中点,M、N分别在边AC、BC上,OM⊥ON,连MN,AC=4,BC=8.设AM=a,BN=b,MN=c
(1) 求证:a2+b2=c2
(2) ① 若a=1,求b;② 探究a与b之间的函数关系式
(3) △CMN的面积的最大值为__________(不写解答过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】小红的父母开了一个小服装店,出售某种进价为![]() 元的服装,现每件
元的服装,现每件![]() 元,每星期可卖
元,每星期可卖![]() 件.该同学对市场作了如下调查:每降价
件.该同学对市场作了如下调查:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件;每涨价
件;每涨价![]() 元,每星期要少卖
元,每星期要少卖![]() 件.
件.
![]() 小红已经求出在涨价情况下一个星期的利润
小红已经求出在涨价情况下一个星期的利润![]() (元)与售价
(元)与售价![]() (元)(
(元)(![]() 为整数)的函数关系式为
为整数)的函数关系式为![]() ,请你求出在降价的情况下
,请你求出在降价的情况下![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为
在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为![]() 元?
元?
![]() 问如何定价,才能使一星期获得的利润最大?
问如何定价,才能使一星期获得的利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=-(a+b)x2-2cx+a-b,a、b、c是△ABC的三边
(1) 当抛物线与x轴只有一个交点时,判断△ABC是什么形状
(2) 当![]() 时,该函数有最大值
时,该函数有最大值![]() ,判断△ABC是什么形状
,判断△ABC是什么形状
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程x2-(k+1)x+![]() k2+1=0
k2+1=0
(1) 当k取何值方程有两个实数根
(2) 是否存在k值使方程的两根为一个矩形的两邻边长,且矩形的对角线长为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与
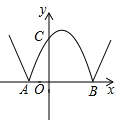
与![]() 轴相交于A,B两点,其顶点为M,将此抛物线在
轴相交于A,B两点,其顶点为M,将此抛物线在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,其余部分保持不变,得到一个新的图像,如图,当直线
轴翻折,其余部分保持不变,得到一个新的图像,如图,当直线![]() 与此图像有且只有两个公共点时,则
与此图像有且只有两个公共点时,则![]() 的取值范围为_____________.
的取值范围为_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如表:则下列判断中正确的是( )
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
A. 抛物线开口向上B. 抛物线与y轴交于负半轴
C. 当x=4时,y>0D. 方程ax2+bx+c=0的正根在3与4之间
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(﹣3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.
(1)求抛物线的解析式;
(2)连接BE,求h为何值时,△BDE的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某通讯器材公司销售一种市场需求较大的新型通讯产品, 已知每件产品的进价为![]() 元,每年销售该产品的总开支(不含进价)总计
元,每年销售该产品的总开支(不含进价)总计![]() 万元,在销售过程中发现,年销售量
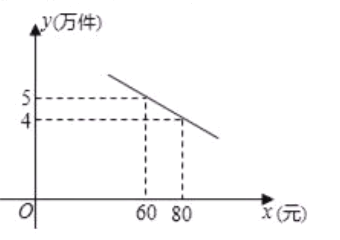
万元,在销售过程中发现,年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间存在如图所示的一次函数关系.
(元)之间存在如图所示的一次函数关系.
(1)求![]() 关于
关于![]() 的函数关系;
的函数关系;
(2)试写出该公司销售该种产品的年获利![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支),当销售单价为何值时年获利最大?并求这个最大值.
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支),当销售单价为何值时年获利最大?并求这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com