
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一条自南向北的大道上有O、A两个景点,O、A相距20km,在O处测得另一景点C位于点O的北偏东37°方向,在A处测得景点C位于点A的南偏东76°方向,且A、C相距13km .
(1)求:①A到OC之间的距离;
②O、C两景点之间的距离;
(2)若在O处测得景点B 位于景点O的正东方向10km,求B、C两景点之间的距离.(参考数据:tan37°=0.75)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长度为5的动线段AB分别与坐标系横轴、纵轴的正半轴交于点A、点B,点O和点C关于AB对称,连接CA、CB,过点C作x轴的垂线段CD,交x轴于点D
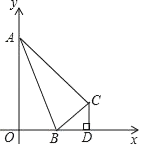
(1)移动点A,发现在某一时刻,△AOB和以点B、D、C为顶点的三角形相似,求这一时刻点C的坐标;
(2)移动点A,当![]() 时求点C的坐标.
时求点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中
中![]() 且
且![]() ,又
,又![]() 、
、![]() 为
为![]() 的三等分点.
的三等分点.

(1)求证![]() ;
;
(2)证明:![]() ;
;
(3)若点![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() 则使线段
则使线段![]() 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=BE=4,AE=3,求CD的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒![]() cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP、PQ、CQ 三者之间的数量关系,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
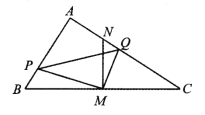
【题目】如图,△ABC 的面积为 63,D 是 BC 上的一点,且 BD:BC=2:3, DE∥AC 交 AB 于点 E,延长 DE 到 F,使 FE:ED=2:1.连结 CF 交 AB 点于 G.
(1)求△BDE 的面积;
(2)求 ![]() 的值;
的值;
(3)求△ACG 的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com