
科目: 来源: 题型:
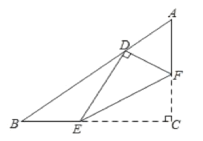
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列条件中,不能判断这个平行四边形是菱形的是( )

A. AB=ADB. ∠BAC=∠DACC. ∠BAC=∠ABDD. AC⊥BD
查看答案和解析>>
科目: 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目: 来源: 题型:
【题目】求解体验:
(1)已知抛物线 y=﹣x2+bx﹣3 经过点(﹣1,0),则 b= ,顶点坐标为 ,该抛物线关于点(0,1)成中心对称的抛物线表达式是 .
抽象感悟:
我们定义:对于抛物线 y=ax2+bx+c(a≠0),以 y 轴上的点 M(0,m)为中心,作该抛物线关于点 M 对称的 抛物线 y′,则我们又称抛物线 y′为抛物线 y 的“衍生抛物线”,点 M 为“衍生中心”.
(2)已知抛物线 y=﹣x2﹣2x+5 关于点(0,m)的衍生抛物线为 y′,若这两条抛物线有交点,求 m 的取值范 围.
问题解决:
(3)已知抛物线 y=ax2+2ax﹣b(a≠0)
①若抛物线 y 的衍生抛物线为 y′=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求 a、b 的值及衍生中心的坐标;
②若抛物线 y 关于点(0,k+12)的衍生抛物线为 y1,其顶点为 A1;关于点(0,k+22)的衍生抛物线为 y2,其顶点为 A2;…;关于点(0,k+n2)的衍生抛物线为 yn,其顶点为 An…(n 为正整数).求 An An+1 的长(用含 n 的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点 C 顺时针旋转,旋转角为0 180 ,得到 ABC
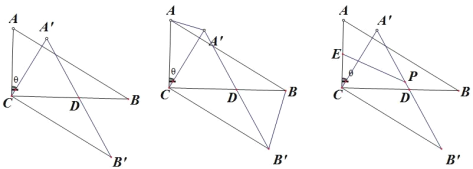
(1)求当角为多少度时, CBD 是等腰三角形;
(2)如图②,连接 AA, BB ,设 ACA , BCB 的面积分别为 S1 , S2 ,求![]() 的值;
的值;
(3)如图③,设 AC 的中点为 E, AB 的中点为 P,AC=a,连接 EP,当旋转角为多少时,EP 长度最大,并求出 EP 的最大值;
查看答案和解析>>
科目: 来源: 题型:
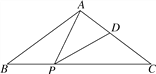
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
科目: 来源: 题型:
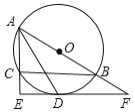
【题目】如图,![]() 是
是![]() ABC的外接圆,AB为直径,∠BAC的平分线交
ABC的外接圆,AB为直径,∠BAC的平分线交![]() 于点D,过点D作DE
于点D,过点D作DE![]() AC分别交AC、AB的延长线于点E、F.
AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是![]() 的切线;
的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留
的长度.(结果保留![]() )
)
查看答案和解析>>
科目: 来源: 题型:
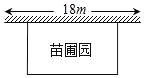
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为 30 米的篱笆 围成.已知墙长为 18 米(如图所示),设这个苗圃园垂直于墙的一边的长为 x 米,若平行于墙的一边长不小 于 8 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com