对数的创始人是苏格兰数学家纳皮尔（J. Nplcr，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707-1783年）才发现指数与对数之间的联系.

对数的定义：一般地，若，那么叫做以为底的对数，记作：.比如指数式可以转化为，对数式可以转化为.

我们根据对数的定义可得到对数的一个性质：；理由如下：

设，，则，

∴，由对数的定义得

又∵

∴

解决以下问题：

（1）将指数转化为对数式______；

（2）证明

（3）拓展运用：计算______.

（1）求证：DE∥BC；

（2）若AF=CE，求线段BC的长度．

（1）此次抽样调查中，共调查了　 　名学生；

（2）将图1、图2补充完整；

（3）现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

（1）求第一、二次购进服装的数量分别是多少件？

（2）由于该款服装刚推出时，很受欢迎，按每件60元销售了x件；后来，由于该服装滞销，为了及时处理库存，缓解资金压力，其剩余部分的按每件30元全部售完．当x的值至少为多少时，该服装商店才不会亏本．

【题目】如图， 抛物线与轴交于点A（-1,0），顶点坐标（1，n）与轴的交点在（0,2），（0,3）之间（包 含端点），则下列结论：①；②；③对于任意实数m，总成立；④关于的方程有两个不相等的实数根．其中结论正确的个数为　　

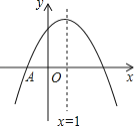
A. 1 个 B. 2 个 C. 3 个 D. 4 个

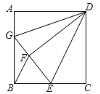
【题目】如图，已知正方形ABCD的边长为6，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①；②；③；④在以上4个结论中，正确的有（ ）

A. 1B. 2C. 3D. 4

【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，… 组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2019秒时，点P的坐标是（ ）

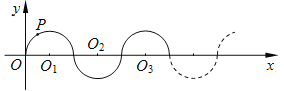
A. （2018，0）B. （2019，1）C. （2019，1）D. （2018，-1）

A. 若y1＜y2，则x1＜x2B. 若y1﹣y2=2，则x1﹣x2=﹣1

C. 可由直线y=2x向上平移4个单位得到D. 与坐标系围成的三角形面积为8

【题目】如图，在菱形ABCD中，、、分别是菱形ABCD的两条对角线长和边长，这时我们把关于的形如“”的一元二次方程称为“菱系一元二次方程”．请解决下列问题：

（1）填空：①当，时， ．

②用含，的代数式表示值， ．

（2）求证：关于的“菱系一元二次方程”必有实数根；

（3）若是“菱系一元二次方程”的一个根，且菱形的面积是25，BE是菱形ABCD的AD边上的高，求BE的值．

（1）问：那么今年年初猪肉的价格为每千克多少元？

（2）某超市将进货价为每千克30元的猪肉，按5月20日价格出售，平均一天能销售出100千克，经调查表明：猪肉的售价每千克下降2元，其日销售量就增加40千克，超市为了实现销售猪肉每天有1120元的销售利润，为了尽可能让顾客优惠应该每千克定价为多少元？