
科目: 来源: 题型:
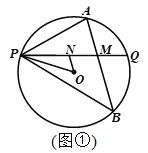
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
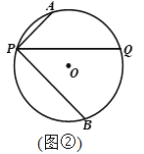
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
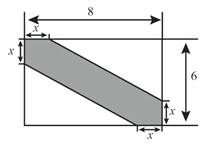
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若△ABC中,其中一个内角是另一个内角的一半,则称△ABC为“半角三角形”.
(1)若Rt△ABC为半角三角形,∠A=90°,则其余两个角的度数为.
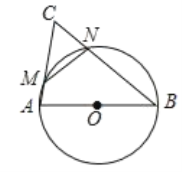
(2)如图,以△ABC的边AB为直径画圆,与边AC交于M,与边BC交于N,已知CN=![]() AC
AC
①求证:∠C=60°.
②若△ABC是半角三角形,求∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
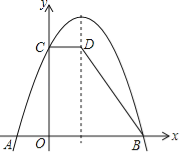
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
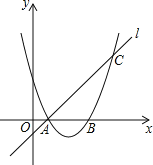
(1)求抛物线的解析式;
(2)设直线l与y轴交于点D,抛物线交y轴于点E,则△DBE的面积是多少?
查看答案和解析>>
科目: 来源: 题型:
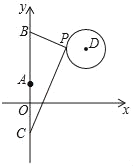
【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,5)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是______________.
查看答案和解析>>
科目: 来源: 题型:
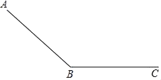
【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270B.280C.375D.450
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,BC=3,以AB为直径的半圆O在矩形ABCD的外部,将半圆O绕点A顺时针旋转a度(0°≤a≤180°).
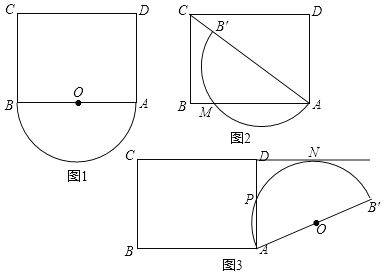
(1)在旋转过程中,B′C的最小值是 ,如图2,当半圆O的直径落在对角线AC上时,设半圆O与AB的交点为M,则AM的长为
(2)如图3,当半圆O与直线CD相切时,切点为N,与线段AD的交点为P,求劣弧AP的长;
(3)在旋转过程中,当半圆弧与直线CD只有一个交点时,设此交点与点C的距离为d,请直接写出d的取值范围.
查看答案和解析>>
科目: 来源: 题型:
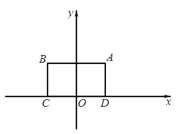
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,它与
,它与![]() 轴、
轴、![]() 轴的交点分别为A、B两点.
轴的交点分别为A、B两点.
(1)求点A、B的坐标;
(2)设F是![]() 轴上一动点,⊙P经过点B且与
轴上一动点,⊙P经过点B且与![]() 轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与
轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与![]() 之间的函数关系;
之间的函数关系;
(3)是否存在这样的⊙P,既与![]() 轴相切,又与直线
轴相切,又与直线![]() 相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.
相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com