
科目: 来源: 题型:
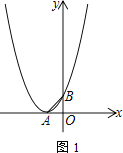
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
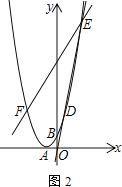
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
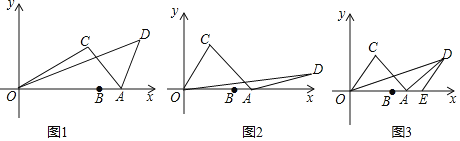
【题目】已知,点![]() 、
、![]() ,将线段
,将线段![]() 绕着原点
绕着原点![]() 逆时针方向旋转角度
逆时针方向旋转角度![]() 到
到![]() ,连接
,连接![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针方向旋转角度
顺时针方向旋转角度![]() 至
至![]() ,连接
,连接![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
(3)已知![]() ,当
,当![]() 时,改变
时,改变![]() 的大小,求
的大小,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
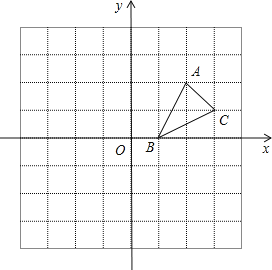
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,三个顶点的坐标分别为
的顶点均在格点上,三个顶点的坐标分别为![]() .
.
(1)将![]() 关于
关于![]() 轴作轴对称变换得
轴作轴对称变换得![]() ,则点
,则点![]() 的坐标为______.
的坐标为______.
(2)将![]() 绕原点
绕原点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得
得![]() ,则点
,则点![]() 的坐标为______.
的坐标为______.
(3)在(1)(2)的基础上,图中的![]() ,
,![]() 是中心对称图形,对称中心的坐标为______.
是中心对称图形,对称中心的坐标为______.
(4)若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,直接写出点
为顶点的四边形为菱形,直接写出点![]() 的坐标为______.
的坐标为______.
查看答案和解析>>
科目: 来源: 题型:
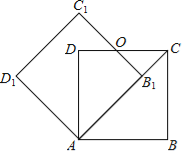
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
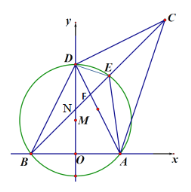
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长;
(4)BC交y轴于点N,问![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
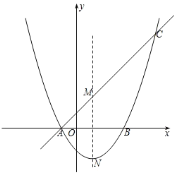
【题目】如图,抛物线![]() 交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
(1)求抛物线的函数关系式;
(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;
(3)在(2)的条件下,求△AQC面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现, 销售量y(件)与销售单价x(元)符合一次函数,所调查的部分数据如表:
销售单价x(元) | 65 | 70 | 80 | … |
销售量y(件) | 55 | 50 | 40 | … |
(1)求出y与x之间的函数表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
(3)销售单价定为多少元时,该商场获得的利润恰为500元?
查看答案和解析>>
科目: 来源: 题型:
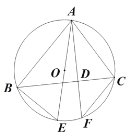
【题目】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为上![]() 一点,且BE=CF,
一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=4,求AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=12,AD平分∠BAC,交BC于点 E,交⊙O于点D,连接BD.
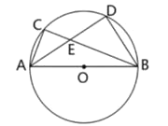
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com