
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,与y轴相交于点C,顶点为P.
,与y轴相交于点C,顶点为P.
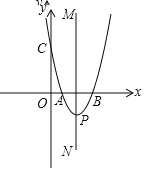
(1)求这条抛物线的表达式和顶点P的坐标;
(2)点E在抛物线的对称轴上,且![]() ,求点E的坐标;
,求点E的坐标;
(3)在(2)的条件下,记抛物线的对称轴为直线MN,点Q在直线MN右侧的抛物线上,![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设![]() (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为
(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为![]() 千米,骑自行车学生骑行的路程为
千米,骑自行车学生骑行的路程为![]() 千米,
千米,![]() 关于
关于![]() 的函数图象如图所示.
的函数图象如图所示.
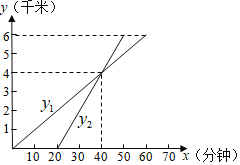
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB的中点,P是直线BC上一点,把△BDP沿PD所在直线翻折后,点B落在点Q处,如果QD⊥BC,那么点P和点B间的距离等于____.
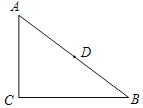
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在半径为2的扇形![]() 中,
中,![]() °,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结
°,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结![]() .
.
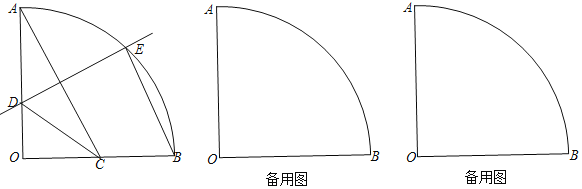
(1)若C是半径OB中点,求![]() 的正弦值;
的正弦值;
(2)若E是弧AB的中点,求证:![]() ;
;
(3)联结CE,当△DCE是以CD为腰的等腰三角形时,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
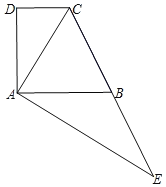
【题目】已知:如图,梯形ABCD,DC∥AB,对角线AC平分∠BCD,点E在边CB的延长线上,EA⊥AC,垂足为点A.
(1)求证:B是EC的中点;
(2)分别延长CD、EA相交于点F,若AC2=DCEC,求证:AD:AF=AC:FC.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校要印刷一批艺术节的宣传资料,在需要支付制版费100元和每份资料0.3元印刷费的前提下,甲、乙两个印刷厂分别提出了不同的优惠条件.甲印刷厂提出:所有资料的印刷费可按9折收费;乙印刷厂提出:凡印刷数量超过200份的,超过部分的印刷费可按8折收费.
(1)设该学校需要印刷艺术节的宣传资料x份,支付甲印刷厂的费用为y元,写出y关于x的函数关系式,并写出它的定义域;
(2)如果该学校需要印刷艺术节的宣传资料600份,那么应该选择哪家印刷厂比较优惠?
查看答案和解析>>
科目: 来源: 题型:
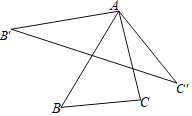
【题目】如图,将![]() 的边
的边![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,边AC绕着点A逆时针旋转
,边AC绕着点A逆时针旋转![]() 得到
得到![]() ,联结
,联结![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“双旋三角形”.如果等边
的“双旋三角形”.如果等边![]() 的边长为a,那么它的“双旋三角形”的面积是__________(用含a的代数式表示).
的边长为a,那么它的“双旋三角形”的面积是__________(用含a的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
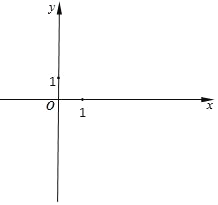
【题目】平面直角坐标系xOy(如图),抛物线y=﹣x2+2mx+3m2(m>0)与x轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线l,过点C作直线l的垂线,垂足为点E,联结DC、BC.
(1)当点C(0,3)时,
①求这条抛物线的表达式和顶点坐标;
②求证:∠DCE=∠BCE;
(2)当CB平分∠DCO时,求m的值.
查看答案和解析>>
科目: 来源: 题型:
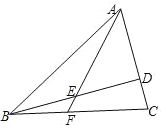
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
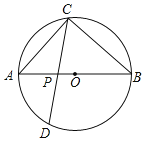
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一点,过点
上一点,过点![]() 作
作![]() 的弦
的弦![]() ,设
,设![]() .
.
(1)若![]() 时,求
时,求![]() 、
、![]() 的度数各是多少?
的度数各是多少?
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,使弦
,使弦![]() 最短?如果存在,求出
最短?如果存在,求出![]() 的值,如果不存在,说明理由;
的值,如果不存在,说明理由;
(3)在(1)的条件下,且![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com