
科目: 来源: 题型:
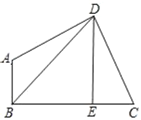
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求点B到CD的距离;
(2)若m=n, BD=3![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点P在∠BCA平分线CD上,且PA=PB.
(1)用尺规作出符合要求的点P(保留作图痕迹,不需要写作法);
(2)判断△ABP的形状(不需要写证明过程)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=![]() x﹣
x﹣![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
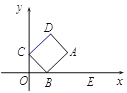
【题目】如图,矩形ABCD的顶点 A的坐标为(4,2),顶点B,C分别在![]() 轴,
轴,![]() 轴的正半轴上.
轴的正半轴上.
(1)求证:∠OCB=∠ABE;
(2)求OC长的取值范围;
(3)若D的坐标为(![]() ,
,![]() ),请说明
),请说明![]() 随
随![]() 的变化情况.
的变化情况.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了更好的落实阳光体育运动,学校需要购买一批足球和篮球,已知一个足球比一个篮球的进价高30元,买一个足球和两个篮球一共需要300元.
(1)求足球和篮球的单价;
(2)学校决定购买足球和篮球共100个,为了加大校园足球活动开展力度,现要求购买的足球不少于60个,且用于购买这批足球和篮球的资金最多为11000元.试设计一个方案,使得用来购买的资金最少,并求出最小资金数.
查看答案和解析>>
科目: 来源: 题型:
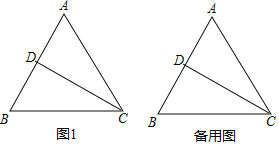
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在线段
在线段![]() 上运动,将线段
上运动,将线段![]() 绕点
绕点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 的对应点
的对应点![]() 落在射线
落在射线![]() 上,连接
上,连接![]() ,设
,设![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,
时,
①在图1中依题意画出图形,并求![]() (用含
(用含![]() 的式子表示);
的式子表示);
②探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(2)当![]() 时,直接写出线段
时,直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
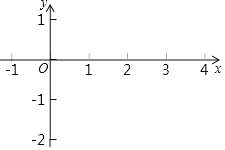
【题目】抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),抛物线的顶点为
左侧),抛物线的顶点为![]() .
.
(1)抛物线![]() 的对称轴是直线________;
的对称轴是直线________;
(2)当![]() 时,求抛物线
时,求抛物线![]() 的函数表达式;
的函数表达式;
(3)在(2)的条件下,直线![]() :
:![]() 经过抛物线的顶点
经过抛物线的顶点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个公共点,它们的横坐标分别记为
有两个公共点,它们的横坐标分别记为![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 的交点的横坐标记为
的交点的横坐标记为![]() ,若当
,若当![]() 时,总有
时,总有![]() ,请结合函数的图象,直接写出
,请结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
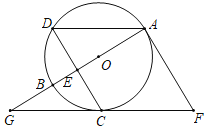
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比
的比![]() 称为点
称为点![]() 的“理想值”,记作
的“理想值”,记作![]() .如
.如![]() 的“理想值”
的“理想值”![]() .
.
(1)①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 等于_______;
等于_______;
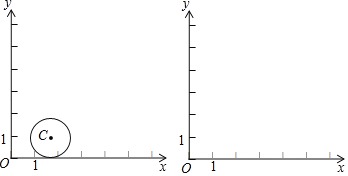
②如图,![]() ,
,![]() 的半径为1.若点
的半径为1.若点![]() 在
在![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 的取值范围是_______.
的取值范围是_______.
(2)点![]() 在直线
在直线![]() 上,
上,![]() 的半径为1,点
的半径为1,点![]() 在
在![]() 上运动时都有
上运动时都有![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(3)![]() ,
,![]() 是以
是以![]() 为半径的
为半径的![]() 上任意一点,当
上任意一点,当![]() 时,画出满足条件的最大圆,并直接写出相应的半径
时,画出满足条件的最大圆,并直接写出相应的半径![]() 的值.(要求画图位置准确,但不必尺规作图)
的值.(要求画图位置准确,但不必尺规作图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com