
科目: 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD为矩形,点E是边BC的中点,AF∥ED,AE∥DF
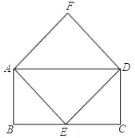
(1)求证:四边形AEDF为菱形;
(2)试探究:当AB:BC= ,菱形AEDF为正方形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市五月遭遇了持续强降雨,造成部分地区洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共4000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用300元购买甲种物品的件数恰好与用240元购买乙种物品的件数相同.
(1)求甲、乙两种救灾物品每件的价格各是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这4000件物品,需筹集资金多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项:评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了________名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为________度;
(3)请将频数分布直方图补充完整;
(4)如果全市有8600名七年级学生,那么在试卷评讲课中,“独立思考”的七年级学生约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】开口向下的抛物线y=a(x+1)(x﹣4)与x轴的交点为A、B(A在B的左边),与y轴交于点C.连接AC、BC.
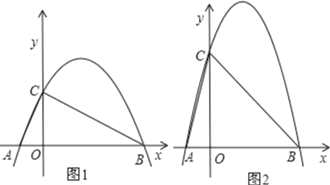
(1)若△ABC是直角三角形(图1),求二次函数的解析式;
(2)在(1)的条件下,将抛物线沿y轴的负半轴向下平移k(k>0)个单位,使平移后的抛物线与坐标轴只有两个交点,求k的值;
(3)当点C坐标为(0,4)时(图2),P、Q两点同时从C点出发,点P沿折线COB运动到点B,点Q沿抛物线(在第一象限的部分)运动到点B,若P、Q两点的运动速度相同,请问谁先到达点B?请说明理由.(参考数据:![]() .6,
.6,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,△ABC为等边三角形,AB=![]() ,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
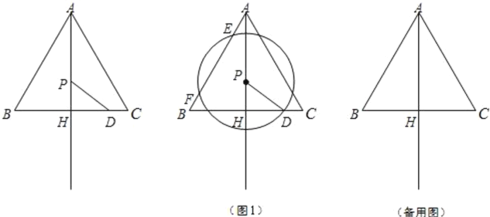
(1)当x=3时,求⊙P的半径长;
(2)如图1,如果⊙P与线段AB相交于E、F两点,且EF=y,求y关于x的函数解析式,并写出它的定义域;
(3)如果△PHD与△ABH相似,求x的值(直接写出答案即可).
查看答案和解析>>
科目: 来源: 题型:
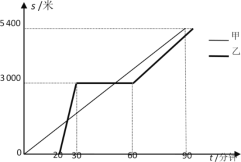
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com