
科目: 来源: 题型:
【题目】如图在矩形![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() ,连接
,连接![]() ,
,![]() . 动点
. 动点![]() 以每秒1个单位的速度从点
以每秒1个单位的速度从点![]() 出发沿
出发沿![]() 向终点
向终点![]() 运动,同时动点
运动,同时动点![]() 以每秒2个单位的速度从点
以每秒2个单位的速度从点![]() 出发沿
出发沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
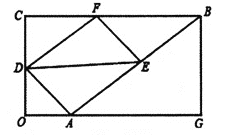
(1)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求证:四边形![]() 为平行四边形;
为平行四边形;
(3)探索当![]() 为何值时,
为何值时,![]() 与以
与以![]() ,
,![]() ,
,![]() 为顶点的三角形相似?
为顶点的三角形相似?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:一元二次方程![]() ,当
,当![]() 时,设两根为
时,设两根为![]() ,
,![]() ,则两根与系数的关系为:
,则两根与系数的关系为:![]() ;
;![]() .
.
应用:
(1)方程![]() 的两实数根分别为
的两实数根分别为![]() ,
,![]() ,则
,则![]() ______,
______,![]() _____;
_____;
(2)若关于![]() 的方程
的方程![]() 的有两个实数根
的有两个实数根![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若满足![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
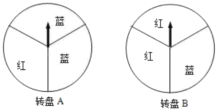
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面内,C为线段AB外的一点,若以A,B,C为顶点的三角形为直角三角形,则称C为线段AB的直角点. 特别地,当该三角形为等腰直角三角形时,称C为线段AB的等腰直角点.
(1)如图1,在平面直角坐标系xOy中,点M的坐标为![]() ,在点P1
,在点P1![]() ,P2
,P2![]() ,P3
,P3![]() 中,线段OM的直角点是 ;
中,线段OM的直角点是 ;
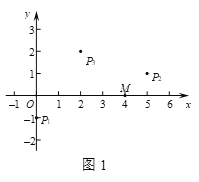
(2)在平面直角坐标系xOy中,点A,B的坐标分别为![]() ,
,![]() ,直线l的解析式为
,直线l的解析式为![]() .
.
①如图2,C是直线l上的一个动点,若C是线段AB的直角点,求点C的坐标;
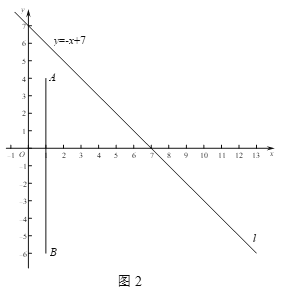
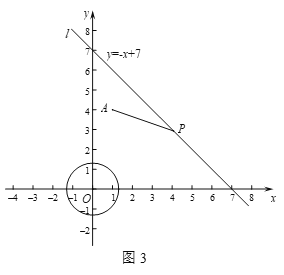
②如图3,P是直线l上的一个动点,将所有线段AP的等腰直角点称为直线l关于点A的伴随点.若⊙O的半径为r,且⊙O上恰有两个点为直线l关于点A的伴随点,直接写出r的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,![]() ,将点C关于直线AB对称得到点D,作射线BD与CA的延长线交于点E,在CB的延长线上取点F,使得BF=DE,连接AF.
,将点C关于直线AB对称得到点D,作射线BD与CA的延长线交于点E,在CB的延长线上取点F,使得BF=DE,连接AF.

备用图
(1)依题意补全图形;
(2)求证:AF=AE;
(3)作BA的延长线与FD的延长线交于点P,写出一个∠ACB的值,使得AP=AF成立,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与直线
与直线![]() 交于A, B两点,其中点A在x轴上.
交于A, B两点,其中点A在x轴上.
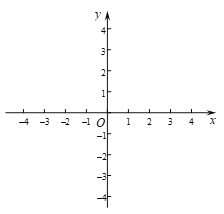
(1)用含有b的代数式表示c;
(2)① 若点B在第一象限,且![]() ,求抛物线的解析式;
,求抛物线的解析式;
② 若![]() ,结合函数图象,直接写出b的取值范围.
,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小娜根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
(1)下表是x与y的几组对应值.
x | … |
|
| 0 |
| 2 |
| 3 | … |
y | … |
|
| 0 | m | n |
| 3 | … |
请直接写出:m= ,n= ;
(2)如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;

(3)结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆(吊杆垂直于桥面),把桥面吊住.某悬索桥(如图1),是连接两个地区的重要通道. 图2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引. 他通过查找资料了解到此桥的相关信息:这座桥的缆索(即图2中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即AB=CD, 两个索塔均与桥面垂直. 主桥AC的长为600 m,引桥CE的长为124 m.缆索最低处的吊杆MN长为3 m,桥面上与点M相距100 m处的吊杆PQ长为13 m.若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端D与锚点E的距离.


图2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,以BC为直径的半圆交AB于点D,O是该半圆所在圆的圆心,E为线段AC上一点,且ED=EA.
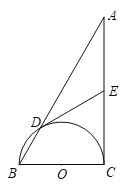
(1)求证:ED是⊙O的切线;
(2)若![]() ,∠A=30°,求⊙O的半径.
,∠A=30°,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com