
科目: 来源: 题型:
【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:如图,过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:如图,
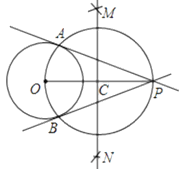
(1)连接OP,作线段OP的垂直平分线MN交OP于点C.
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点.
(3)作直线PA,PB.
所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:
(1)连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_________.
(2)如果⊙O的半径等于3,点P到切点的距离为4,求点A与点B之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是_____度,阴影部分的面积为_____.
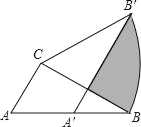
查看答案和解析>>
科目: 来源: 题型:
【题目】若抛物线y=(x﹣2m)2+3m﹣1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是( )
A.m<2B.m>2C.m![]() D.m
D.m![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在一张矩形纸片![]() 中,
中,![]() ,
,![]() ,现将这张纸片按下列图示方法折叠,请解决下列问题:
,现将这张纸片按下列图示方法折叠,请解决下列问题:
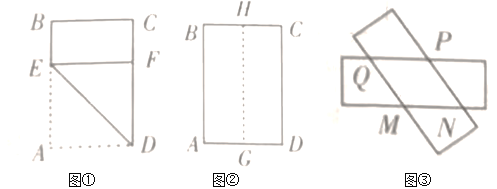
(1)如图①,折痕为![]() ,点
,点![]() 的对应点
的对应点![]() 在
在![]() 上,求证:四边形
上,求证:四边形![]() 是正方形;
是正方形;
(2)如图②,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,把矩形纸片
的中点,把矩形纸片![]() 沿着
沿着![]() 剪开,变成两张矩形纸片,将两张纸片任意叠合后(如图③),判断重叠四边形
剪开,变成两张矩形纸片,将两张纸片任意叠合后(如图③),判断重叠四边形![]() 的形状,并证明;
的形状,并证明;
(3)在(2)中,重叠四边形![]() 的周长是否存在最大值或最小值?若存在,请求出最大值或最小值;若不存在,请说明理由.
的周长是否存在最大值或最小值?若存在,请求出最大值或最小值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在![]() 的网格图中,每个小正方形的边长均为
的网格图中,每个小正方形的边长均为![]() ,点
,点![]() 和
和![]() 的顶点均为小正方形的顶点.
的顶点均为小正方形的顶点.
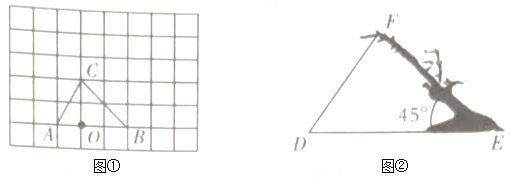
(1)以点O为位似中心,在网格图中作△ABC,使它与△ABC位似,且相似比为2;
(2)如图②,某台风过后,李明发现一棵被吹倾斜的大树![]() 与地面的夹角为
与地面的夹角为![]() ,且其影子
,且其影子![]() 长为4.5米,同时李明还发现大树树干和影子形成的△DEF与△ABC相似(树干对应
长为4.5米,同时李明还发现大树树干和影子形成的△DEF与△ABC相似(树干对应![]() 边),求大树在被吹倾斜前的高度.(结果保留根号)
边),求大树在被吹倾斜前的高度.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】奇思参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题奇思都不会,不过奇思还有两个“求助”可以使用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果奇思两次“求助”都在第一道单选题中使用,求他通关的概率;
(2)如果奇思每道单选题各使用一次“求助",请用列表法或画树状图的方法求他顺利通关的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为![]() ,连接CF,则CF= .
,连接CF,则CF= .

查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线的顶点H(2,0),经过点A(1,1),与y轴交于点C.

(1)求抛物线的解析式;
(2)如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;
(3)如图2,过点P(﹣3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PMPN的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,若四边形ABCD、GFED都是正方形,显然图中有AG=CE,AG⊥CE.
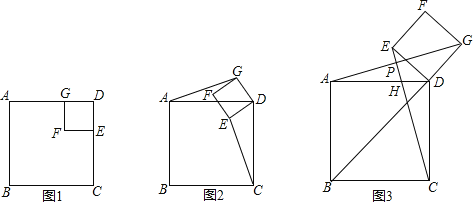
(1)当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明,若不成立,请说明理由;
(2)当正方形GFED绕D旋转到B,D,G在一条直线(如图3)上时,连结CE,设CE分别交AG、AD于P、H.
①求证:AG⊥CE;
②如果,AD=2![]() ,DG=
,DG=![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com