
科目: 来源: 题型:
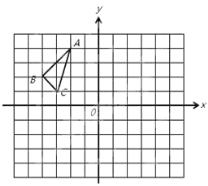
【题目】△ABC 在平面直角坐标系中的位置如图所示,其中每 个小正方形的边长为 1 个单位长度.
(1)画出△ABC 关于原点 O 的中心对称图形△A1B1C1,并写出点 A1 的坐标;
(2)将△ABC 绕点 C 顺时针旋转 90°得到△A2B2C,画出△A2B2C,求在旋转过程中,点 A 所经过的路径长
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
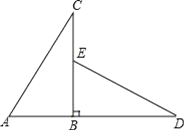
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
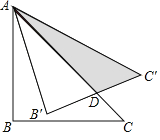
【题目】如图,等腰直角三角形ABC的直角边AB的长为![]() ,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于( )
,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系上,已知点 A(8,4),AB⊥y轴于 B,AC⊥x轴于 C,直线 y=x交 AB于 D.
(1)如图 1,若 E 为 OD 延长线上一动点,当△BCE 的面积,S△BCE=20 时,过点 E 作 EF⊥AB于 F,点 G、H 分别为 AC、CB 上动点,求 FG+GH 的最小值及点 G 的坐标.
(2)如图 2,直线 BC 与 DE 交于点 M,作直线 MN∥y 轴,在(1)的条件下,将△DEF 沿 DE方向平移![]() 个单位得到△D′E′F′,在直线 MN 上是否存在点 P 使得△BF′P 为等腰三角形,若存在请直接写出满足条件的点 P 的坐标;若不存在,请说明理由.
个单位得到△D′E′F′,在直线 MN 上是否存在点 P 使得△BF′P 为等腰三角形,若存在请直接写出满足条件的点 P 的坐标;若不存在,请说明理由. 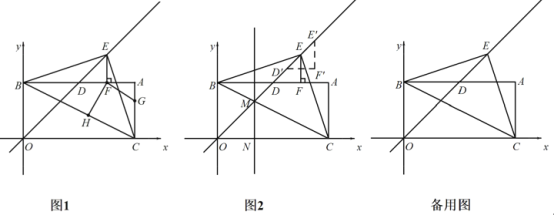
查看答案和解析>>
科目: 来源: 题型:
【题目】在ABCD 中,∠BAD 的平分线交直线 BC 于点 E,交直线 DC 于点 F,∠D=120°.
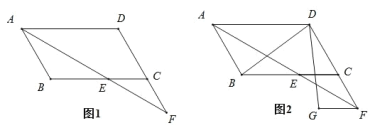
(1)如图 1,若 AD=6,求△ADF 的面积;
(2)如图 2,过点 F 作 FG∥CE,FG=CE,连结 DB、DG,求证:BD=DG.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年以来猪肉价格不断走高,引起了民众与区政府的高度关注,当市场猪肉的平均价格每 千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.据统计:从今年年初至 11月 10 日,猪排骨价格不断走高,11 月 10 日比年初价格上涨了 75%.今年 11 月 10 日某市 民于 A 超市购买 5 千克猪排骨花费 350 元.
(1)A 超市 11 月排骨的进货价为年初排骨售价的![]() 倍,按 11 月 10 日价格出售,平均一天能销售出 100 千克,超市统计发现:若排骨的售价每千克下降 1 元,其日销售量就增加 20千克,超市为了实现销售排骨每天有 1000 元的利润,为了尽可能让顾客优惠应该将排骨的 售价定位为每千克多少元?
倍,按 11 月 10 日价格出售,平均一天能销售出 100 千克,超市统计发现:若排骨的售价每千克下降 1 元,其日销售量就增加 20千克,超市为了实现销售排骨每天有 1000 元的利润,为了尽可能让顾客优惠应该将排骨的 售价定位为每千克多少元?
(2)11 月 11 日,区政府决定投入储备猪肉并规定排骨在 11 月 10 日售价的基础上下调 a%出售,A 超市按规定价出售一批储备排骨,该超市在非储备排骨的价格不变情况下,该天的两种猪排骨总销量比 11 月 10 日增加了 a%,且储备排骨的销量占总销量的![]() ,两种排骨销售的总金额比 11 月 10 日提高了
,两种排骨销售的总金额比 11 月 10 日提高了![]() a%,求 a 的值.
a%,求 a 的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】参照学习反比例函数的过程与方法,探究函数 y1=![]() (x≠0)的图象与性质,因为 y1=
(x≠0)的图象与性质,因为 y1=![]() =1﹣
=1﹣![]() ,即 y1=﹣
,即 y1=﹣![]() +1,所以我们对比函数 y=﹣
+1,所以我们对比函数 y=﹣![]() 来探究画出函数 y1=
来探究画出函数 y1=![]() (x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
(x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
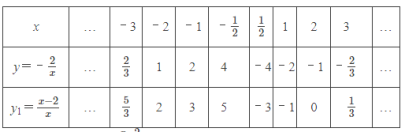
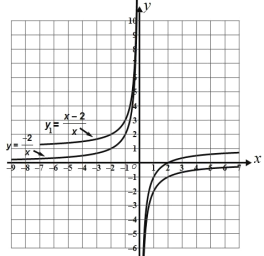
(1)观察:由 y1=![]() 图象可知:
图象可知:
①当 x>0 时,y 随 x的增大而 (填“增大”或“减小”)
②y1=![]() 的图象可以由 y=﹣
的图象可以由 y=﹣![]() 的图象向 平移 个单位长度得到.
的图象向 平移 个单位长度得到.
③y1 的取值范围是 .
(2)探究:①若直线 l 对应的函数关系式为 y2=kx+b,且经过点(﹣1,3)和点(1,﹣1),请再给出的平面直角坐标系中画出 y2,若 y1>y2,则 x 的取值范围为 .
②A(m1,n1),B(m2,n2)在函数 y=![]() 图象上,且 n1+n2=2,求 m1+m2 的值.
图象上,且 n1+n2=2,求 m1+m2 的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生每天的睡眠情况,万州二中初三年级从 1040 名学生中随机抽取了 40 名学生, 调查了他们平均每天的睡眠时间(单位:h),统计结果如下: 7,7,7,7.5,7.5,7.5,7.5,8,8,8,8,8,8,8.5,8.5,8.5,8.5,8.5,9,9,
9,9,9,9,9,9,9,9,9,9.5,9.5,9.5,9.5,9.5,9.5,9.5,10,10,10,10.5.
在对这些数据整理后,绘制了如下的统计图表:
分组统计表
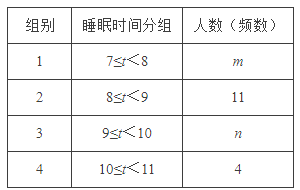

请根据以上信息,解答下列问题:
(1)m= ,n= ,a= ,b= ,抽取的这 40 名学生平均每天 睡眠时间的中位数落在 组(填组别);
(2)如果按照学校要求,学生平均每天的睡眠时间应不少于 9h,请估计该校学生中睡眠时 间符合要求的人数;
(3)分析以上数据,评价本年级学生的睡眠情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com