
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°
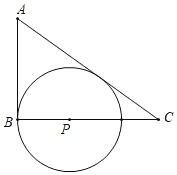
(1)在BC边上找一点P,作⊙P与AC,AB边都相切,与AC的切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=4,AC=6,求第(1)题中所作圆的半径;
(3)连接BQ,第(2)题中的条件不变,求cos∠CBQ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O在ABCD的AD边上,⊙O经过A、B、C三点,点E在⊙O外,且OE⊥BC,垂足为F.
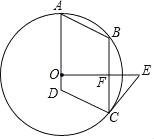
(1)若EC是⊙O的切线,∠A=65°,求∠ECB的度数;
(2)若OF=4,OD=1,求AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0.
(1)当方程有一个根为﹣1时,求k的值及另一个根;
(2)当方程有两个不相等的实数根,求k的取值范围;
(3)若方程两实根x1、x2满足x1+x2=x1x2,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE,GF⊥EF,支架可绕点O旋转,OE=20cm,EF=20![]() cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)求FG的长度(结果精确到0.1);
(2)将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)

查看答案和解析>>
科目: 来源: 题型:
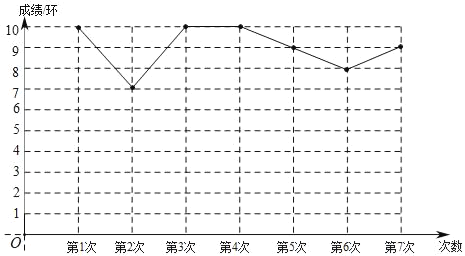
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
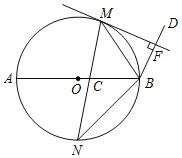
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于C,M为此抛物线的顶点.
与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于C,M为此抛物线的顶点.
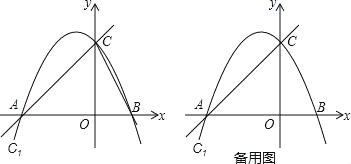
(1)求此抛物线的函数解析式;
(2)动直线l从与直线AC重合的位置出发,绕点A顺时针旋转,与直线AB重合时终止运动,直线l与BC交于点D,P是线段AD的中点.
①直接写出点P所经过的路线长为 ;
②点D与B、C不重合时,过点D作DE⊥AC于点E,作DF⊥AB于点F,连接PE、PF、EF,在旋转过程中,求EF的最小值;
(3)将抛物线C1平移得到抛物线C2,已知抛物线C2的顶点为N,与直线AC交于E、F两点,若EF=AC,求直线MN的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
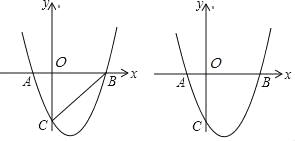
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
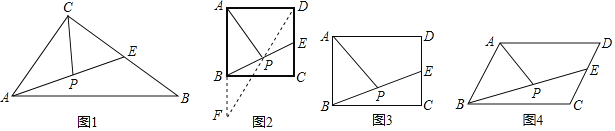
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com