
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,![]() ),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
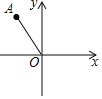
A.(0,﹣2)B.(1,﹣![]() )C.(2,0)D.(
)C.(2,0)D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=20°.将△ABC绕点C按逆时针方向旋转得△A′B′C,且点B在A′B′ 上,CA′ 交AB于点D,则∠BDC的度数为( )

A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目: 来源: 题型:
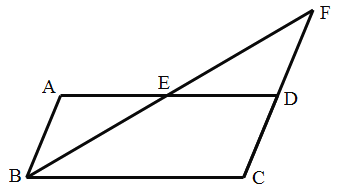
【题目】如图,在□ABCD中,E是AD边上的中点,连接BE并延长交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)![]()
(2)![]()
(3)(6x-1)2-25=0
(4)![]()
(5) ![]()
(6) ![]()
(7)![]() +
+![]() +(﹣1)0﹣2sin45°
+(﹣1)0﹣2sin45°
(8)6tan230°-cos30°·tan60°-2sin 45°+cos60°.
查看答案和解析>>
科目: 来源: 题型:
【题目】基础知识考查:
(1)一次函数表达式 ,当k>0,b>0时,图像经过 象限;当k>0,b<0时,图像经过 象限;当k<0,b>0时,图像经过 象限;当k<0,b<0时,图像经过 象限.特别当b=0时,图像经过 ,称为 函数.
(2)反比例函数三种表达方式分别为: 、 、 反比例函数的图像称为 ,当k>0时,图像在 和 象限,y随x的增大而 ;当k<0时,图像在 和 象限,y随x的增大而 .
(3)特殊三角函数值:
0° | 30° | 45° | 60° | 90° | |
sinA | |||||
cosA | |||||
tanA | |||||
cotA |
(4)二次函数表达式:
①一般式: ;
②顶点式: ; ; ;
.
③交点式(点式): ;
④对称轴公式: 顶点坐标公式: .
⑤二次函数图像称为 ,当a>0时,图像开口向 ;当a<0时,图像开口向 .c>0时,图像和 轴正半轴相交,c<0时,图像和 轴负半轴相交.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,已知抛物线经过坐标原点O和 ![]() 轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在
轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在 ![]() 轴的负半轴、
轴的负半轴、 ![]() 轴的正半轴上,且AD=2,AB=3.
轴的正半轴上,且AD=2,AB=3.
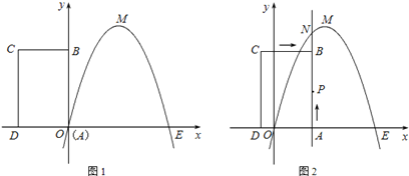
(1)求该抛物线的函数关系式;
(2)如图1,将矩形ABCD以每秒1个单位长度的速度从所示的位置沿 ![]() 轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为
轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为![]() 秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①直接写出P点坐标。(用含t的代数式表示)
②当t为多少时,P、N两点重合?
③设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】好山好水好江山,石拱桥在江山处处可见,小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面宽度16m时,拱顶高出水平 面4m,货船宽12m,船舱顶部为矩形并高出水面3m。
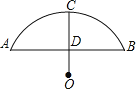
(1)请你帮助小明求此圆弧形拱桥的半径;
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com