
科目: 来源: 题型:
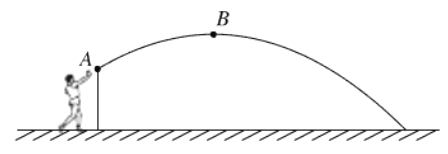
【题目】为了在校运会中取得更好的成绩,小丁积极训练.在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是![]() 米,当铅球运行的水平距离为3米时,达到最大高度
米,当铅球运行的水平距离为3米时,达到最大高度![]() 的B处.小丁此次投掷的成绩是多少米?
的B处.小丁此次投掷的成绩是多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.
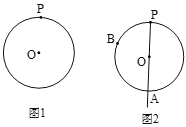
已知:如图1,![]() 及
及![]() 上一点P.
上一点P.
求作:直线PQ,使得PQ与![]() 相切.
相切.
作法:如图2,
①连接PO并延长交![]() 于点A;
于点A;
②在![]() 上任取一点B(点P,A除外),以点B为圆心,BP长为半径作
上任取一点B(点P,A除外),以点B为圆心,BP长为半径作![]() ,与射线PO的另一个交点为C.
,与射线PO的另一个交点为C.
③连接CB并延长交![]() 于点Q.
于点Q.
④作直线PQ;
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图的过程.
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明.
证明:∵CQ是的![]() 直径,
直径,
∴![]() ________
________![]() (________________)(填推理的依据)
(________________)(填推理的依据)
∴![]() .
.
又∵OP是![]() 的半径,
的半径,
∴PQ是![]() 的切线(________________)(填推理的依据)
的切线(________________)(填推理的依据)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数![]() 的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
(1)直接写出点A,C,P的坐标.
(2)画出这个函数的图象.
查看答案和解析>>
科目: 来源: 题型:
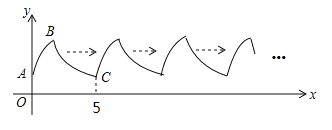
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
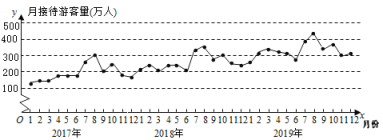
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,年接待旅游量逐年增加
B.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
C.2019年的月接待旅游量的平均值超过300万人次
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
科目: 来源: 题型:
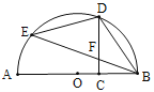
【题目】如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①![]() ,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
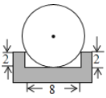
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④
查看答案和解析>>
科目: 来源: 题型:
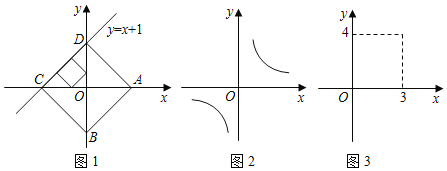
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A.B.C.D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“和谐正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“和谐正方形”.
(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“和谐正方形”的边长;
(2)如图2,若某函数是反比例函数y=![]() (k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“和谐正方形”为ABCD,C、D中的一个点坐标为(3,4),请求出该二次函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
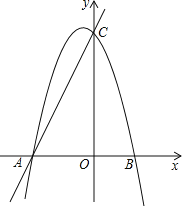
【题目】如图所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=﹣x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=﹣![]() 时,y取最大值
时,y取最大值![]() .
.
(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1:3,求点P的坐标;
(3)若直线y=![]() x+a与(1)中所求的抛物线交于M、N两点,问:
x+a与(1)中所求的抛物线交于M、N两点,问:
①是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由;
②猜想当∠MON>90°时,a的取值范围(不写过程,直接写结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com