
科目: 来源: 题型:
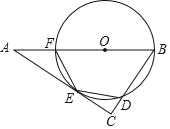
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知矩形ABCD中,AB=2,BC=m,点E是边BC上一点,BE=1,连接AE,沿AE翻折△ABE使点B落在点F处.
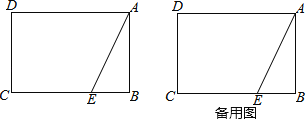
(1)连接CF,若CF∥AE,求m的值;
(2)连接DF,若![]() ≤DF≤
≤DF≤![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
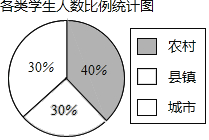
【题目】某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
各类学生成绩人数比例统计表
等第 人数 类别 | A | B | C | D |
农村 | 200 | 240 | 80 | |
县镇 | 290 | 132 | 130 | |
城市 | 240 | 132 | 48 |
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有15000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).

查看答案和解析>>
科目: 来源: 题型:
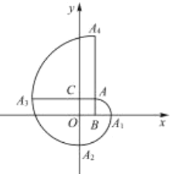
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧.继续以点
为半径的圆弧.继续以点![]() ,
,![]() ,
,![]() ,
,![]() 为圆心按上述作法得到的曲线
为圆心按上述作法得到的曲线![]() …称为正方形的“渐开线”,则点
…称为正方形的“渐开线”,则点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A、B、C三点均在二次函数y=x2的图象上,M为线段AC的中点,BM∥y轴,且MB=2.设A、C两点的横坐标分别为t1、t2(t2>t1),则t2﹣t1的值为( )
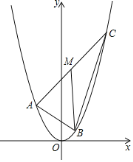
A.3B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
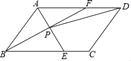
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() (
(![]() 在
在![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)如图1,点![]() 是直线
是直线![]() 上方抛物线上一点,当
上方抛物线上一点,当![]() 面积最大时,点
面积最大时,点![]() 分别为
分别为![]() 轴上的动点,连接
轴上的动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 的周长最小值;
的周长最小值;
(2)如图2,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,将抛物线沿射线
,将抛物线沿射线![]() 的方向平移得到新的拋物线
的方向平移得到新的拋物线![]() ,使得
,使得![]() 交
交![]() 轴于点
轴于点![]() (
(![]() 在
在![]() 的左侧). 将
的左侧). 将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() . 抛物线
. 抛物线![]() 的对称轴上有—动点
的对称轴上有—动点![]() ,坐标系内是否存在一点
,坐标系内是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,若存在,请直接写出点
为顶点的四边形是菱形,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:求解一元一次方程,需要根据等式的基本性质,把方程转化为![]() 的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为连个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解;各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想——转化,即把未知转化为已知来求解.
的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为连个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解;各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想——转化,即把未知转化为已知来求解.
用“转化”的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程![]() ,通过因式分解把它转化为
,通过因式分解把它转化为![]() ,通过解方程
,通过解方程![]() 和
和![]() ,可得原方程
,可得原方程![]() 的解.
的解.
再例如,解根号下含有来知数的方程:![]() ,通过两边同时平方把它转化为
,通过两边同时平方把它转化为![]() ,解得:
,解得:![]() . 因为
. 因为![]() ,且
,且![]() ,所以
,所以![]() 不是原方程的根,
不是原方程的根,![]() 是原方程的解.
是原方程的解.
(1)问题:方程![]() 的解是
的解是![]() ,
,![]() __________,
__________,![]() __________;
__________;
(2)拓展:求方程![]() 的解.
的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com