
科目: 来源: 题型:
【题目】如图,已知反比例函数![]() 和一次函数
和一次函数![]() 的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
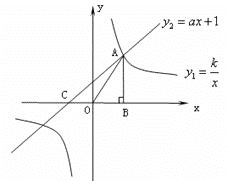
(1)求反比例函数和一次函数的解析式.
(2)若一次函数![]() 的图象与x轴相交于点C,求∠ACO的度数.
的图象与x轴相交于点C,求∠ACO的度数.
(3)结合图象直接写出:当![]() >
>![]() >0时,x的取值范围.
>0时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
科目: 来源: 题型:
【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题:
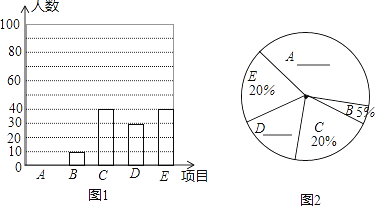
(1)在这项调查中,共调查了_______名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,给出如下定义:若点
中,给出如下定义:若点![]() 在图形
在图形![]() 上,点
上,点![]() 在图形
在图形![]() 上,如果
上,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 的“近距离”,记为
的“近距离”,记为![]() .特别地,当图形
.特别地,当图形![]() 与图形
与图形![]() 有公共点时,
有公共点时,![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,
(1)![]() 点
点![]() ,点
,点![]()
![]() ,
,![]() 点
点![]() ,线段
,线段![]()
![]() ;
;
(2)⊙![]() 半径为
半径为![]() ,
,
①当![]() 时,求⊙
时,求⊙![]() 与线段
与线段![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,线段
,线段![]() ;
;
②若![]() ⊙
⊙![]() ,
,![]()
![]() ,则
,则![]() .
.
(3)![]() 为
为![]() 轴上一点,⊙
轴上一点,⊙![]() 的半径为1,点
的半径为1,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,⊙
,⊙![]() 与
与![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,
,![]() ,请直接写出圆心
,请直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
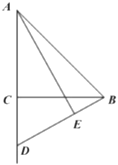
(1)求证:![]() .
.
(2)将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,所得的射线与线段
后,所得的射线与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
①依题意补全图形;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
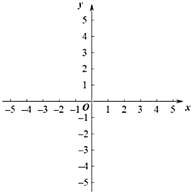
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
工厂加工某种新型材料,首先要将材料进行加温处理,使这种材料保持在一定的温度范围内方可进行继续加工![]() 处理这种材料时,材料温度
处理这种材料时,材料温度![]() 是时间
是时间![]() 的函数
的函数![]() 下面是小明同学研究该函数的过程,把它补充完整:
下面是小明同学研究该函数的过程,把它补充完整:
![]() 在这个函数关系中,自变量x的取值范围是______.
在这个函数关系中,自变量x的取值范围是______.
![]() 如表记录了17min内10个时间点材料温度y随时间x变化的情况:
如表记录了17min内10个时间点材料温度y随时间x变化的情况:
时间 | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|
温度 | 15 | 24 | 42 | 60 |
|
|
|
| m |
|
|
上表中m的值为______.
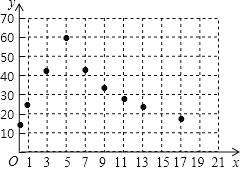
![]() 如图,在平面直角坐标系xOy中,已经描出了上表中的部分点
如图,在平面直角坐标系xOy中,已经描出了上表中的部分点![]() 根据描出的点,画出该函数的图象.
根据描出的点,画出该函数的图象.
![]() 根据列出的表格和所画的函数图象,可以得到,当
根据列出的表格和所画的函数图象,可以得到,当![]() 时,y与x之间的函数表达式为______,当
时,y与x之间的函数表达式为______,当![]() 时,y与x之间的函数表达式为______.
时,y与x之间的函数表达式为______.
![]() 根据工艺的要求,当材料的温度不低于
根据工艺的要求,当材料的温度不低于![]() 时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.
时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com