
科目: 来源: 题型:
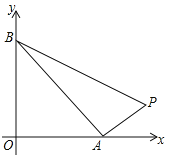
【题目】如图,由点P(14,1),A(![]() ,0),B(0,
,0),B(0,![]() )(
)(![]() ),确定的△PAB的面积为18,则
),确定的△PAB的面积为18,则![]() 的值为_________,如果
的值为_________,如果![]() ,则
,则![]() 的值为_____________________
的值为_____________________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为![]() 、
、![]() 、
、![]() ,若AD=2,AB=
,若AD=2,AB=![]() ,∠A=60°,则
,∠A=60°,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目: 来源: 题型:
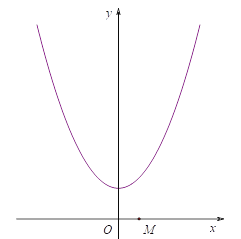
【题目】将抛物线![]() 向左平移2个单位,再向上平移4个单位得到一个新的抛物线.
向左平移2个单位,再向上平移4个单位得到一个新的抛物线.
(1)求新的抛物线的解析式.
(2)过![]() 作直线
作直线![]() ,使得直线
,使得直线![]() 与新的抛物线仅有一个公共点,求直线
与新的抛物线仅有一个公共点,求直线![]() 的解析式及相应公共点的坐标.
的解析式及相应公共点的坐标.
(3)请猜想在新的抛物线上是否有且仅有四个点![]() 、
、![]() 、
、![]() 、
、![]() 使得
使得![]() 、
、![]() 、
、![]() 、
、![]() 分别与(2)中的所有公共点所围成的图形的面积均为S?若有,请求出S并直接写出
分别与(2)中的所有公共点所围成的图形的面积均为S?若有,请求出S并直接写出![]() 、
、![]() 、
、![]() 、
、![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需650万元;若购买A型公交车3辆,B型公交车2辆,共需600万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于830万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目: 来源: 题型:
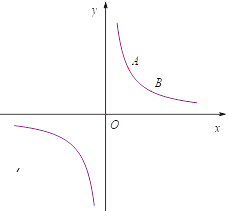
【题目】如图所示,已知![]() 点的横坐标为2,将
点的横坐标为2,将![]() 点向右平移2个单位,再向下平移2个单位得到
点向右平移2个单位,再向下平移2个单位得到![]() 点,且
点,且![]() 、
、![]() 两点均在双曲线
两点均在双曲线![]() 上.
上.
(1)求反比例函数的解析式.(2)若直线![]() 于反比例函数
于反比例函数![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了解七年级400名学生读书情况,随机调查了七年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数;
(2)根据样本数据,估计该校七年级400名学生在本次活动中读书多于3册的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
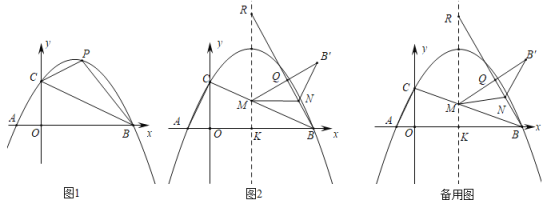
(1)点P为线段BC上方抛物线上(不与B、C重合)的一动点,连接PC、PB,当△PBC面积最大时,在y轴找点D,使得PD﹣![]() OD的值最小时,求这个最小值.
OD的值最小时,求这个最小值.
(2)如图2,抛物线对称轴与x轴交于点K,与线段BC交于点M,在对称轴上取一点R,使得KR=12(点R在第一象限),连接BR.已知点N为线段BR上一动点,连接MN,将△BMN沿MN翻折到△B'MN.当△B'MN与△BMR重叠部分(如图中的△MNQ)为直角三角形时,直接写出此时点B'的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.
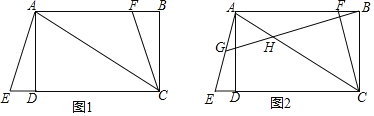
(1)若DE=1,CF=![]() ,求CD的长;
,求CD的长;
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=![]() AC.
AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com