
科目: 来源: 题型:
【题目】综合与实践
问题情境
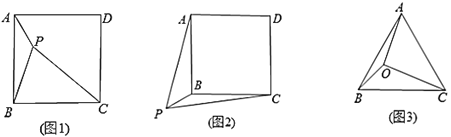
数学课上,李老师提出了这样一个问题:如图1,点![]() 是正方形
是正方形![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() .你能求出
.你能求出![]() 的度数吗?
的度数吗?
(1)小敏与同桌小聪通过观察、思考、讨论后,得出了如下思路:
思路一:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,求出
,求出![]() 的度数.
的度数.
思路二:将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,求出
,求出![]() 的度数.
的度数.
请参考以上思路,任选一种写出完整的解答过程.
类比探究
(2)如图2,若点![]() 是正方形
是正方形![]() 外一点,
外一点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
拓展应用
(3)如图3,在边长为![]() 的等边三角形
的等边三角形![]() 内有一点
内有一点![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积是______.
的面积是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
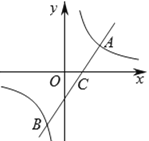
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,点
,点![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .
.
(1)求![]() 、
、![]() 的值.
的值.
(2)请根据图象直接写出不等式![]() 的解集.
的解集.
(3)![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是
三点为顶点的三角形是![]() 为腰的等腰三角形,若存在,请直接写出符合条件的点
为腰的等腰三角形,若存在,请直接写出符合条件的点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士.如图是四位院士(依次记为![]() 、
、![]() 、
、![]() 、
、![]() ).为让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上
).为让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上![]() 、
、![]() 、
、![]() 、
、![]() 四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料,并做成小报.
四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料,并做成小报.
(1)班长在四种卡片中随机抽到标号为C的概率为______.
(2)请用画树状图或列表的方法求小明和小华查找不同院士资料的概率.

查看答案和解析>>
科目: 来源: 题型:
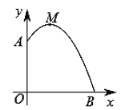
【题目】如图,某幢建筑物从2.25米高的窗口![]() 用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点
用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点![]() 离墙1米,离地面3米,则水流下落点
离墙1米,离地面3米,则水流下落点![]() 离墙的距离
离墙的距离![]() 是( )
是( )
A.2.5米B.3米C.3.5米D.4米
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果一个一元二次方程的两个实数根的比值与另一个一元二次方程的两个实数根的比值相等,我们称这两个方程为“相似方程”,例如,![]() 的实数根是3或6,
的实数根是3或6,![]() 的实数根是1或2,
的实数根是1或2,![]() ,则一元二次方程
,则一元二次方程![]() 与
与![]() 为相似方程.下列各组方程不是相似方程的是( )
为相似方程.下列各组方程不是相似方程的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.

(1)求二次函数![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 平行于
平行于![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 为抛物线上的一点(点
为抛物线上的一点(点![]() 在
在![]() 上方),作
上方),作![]() 平行于
平行于![]() 轴交
轴交![]() 于点
于点![]() ,当点
,当点![]() 在何位置时,四边形
在何位置时,四边形![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com