【题目】某商场将每件进价为20元的玩具以30元的价格出售时，每天可售出300件.经调查当单价每涨l元时，每天少售出10件.若商场想每天获得3750元利润，设每件玩具涨元，可列方程为：.对所列方程中出现的代数式，下列说法错误的是（ ）

A.表示涨价后玩具的单价

B.表示涨价后少售出玩具的数量

C.表示涨价后销售玩具的数量

D.表示涨价后的每件玩具的单价

（1）写出点M所有可能的坐标；

（2）求点M在直线上的概率．

经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．

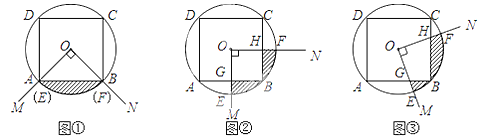
如图，正方形ABCD内接于⊙O，⊙O的面积为S1，正方形ABCD的面积为S2．以圆心O为顶点作∠MON，使∠MON＝90°．将∠MON绕点O旋转，OM、ON分别与⊙O交于点E、F，分别与正方形ABCD的边交于点G、H．设由OE、OF、及正方形ABCD的边围成的图形(阴影部分)的面积为S．

（1）当OM经过点A时(如图①)，则S、S1、S2之间的关系为： (用含S1、S2的代数式表示)；

（2）当OM⊥AB于G时(如图②)，则(1)中的结论仍然成立吗？请说明理由；

（3）当∠MON旋转到任意位置时（如图③），则（1）中的结论任然成立吗：请说明理由.

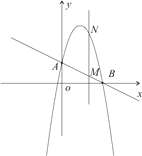
【题目】如图，一次函数分别交y轴、x 轴于A、B两点，抛物线过A、B两点。（1）求这个抛物线的解析式；（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N。求当t 取何值时，MN有最大值？最大值是多少？

【题目】(本小题满分7分) 已知：如图，A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC=BC，AC=OB．

（1）求证：AB是⊙O的切线；

（2）若∠ACD=45°，OC=2，求弦CD的长．

【题目】如图，在边长为2的正方形中，动点，分别以相同的速度从，两点同时出发向和运动(任何一个点到达停止)，在运动过程中，则线段的最小值为________．

A.“概率为0．0001的事件”是不可能事件

B.任意掷一枚质地均匀的硬币10次，正面向上的一定是5次

C.“任意画出一个等边三角形，它是轴对称图形”是随机事件

D.“任意画出一个平行四边行，它是中心对称图形”是必然事件

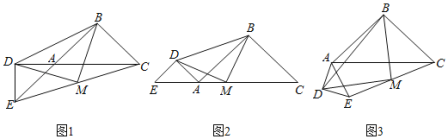
（1）如图1，当点D在CA延长线上时，点M为EC的中点，求证：△DMB是等腰三角形．

（2）如图2，当点E在CA延长线上时，M是EC上一点，若△DMB是等腰直角三角形，∠DMB为直角，求证：点M是EC的中点．

（3）如图3，当△ADE绕点A旋转任意角度时，线段EC上是否都存在点M，使△BMD为等腰直角三角形，若不存在，请举出反例；若存在，请予以证明．