
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为![]() 的中点.
的中点.
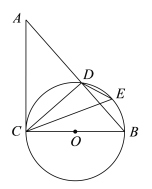
(1)求证:∠ACD=∠DEC;(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于E.
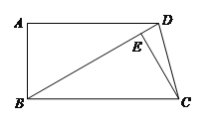
(1)求证:BE=AD;(2)若∠DCE=15°,AB=2,求在四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.

已知:△ABC.
求作:BC边上的高线.
作法:如图,
①分别以A,B为圆心,大于![]() 长为半径画弧,两弧交于点D,E;
长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上( )(填推理的依据).
∵ = ,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90°( )(填推理的依据).
∴AG⊥BC
即AG就是BC边上的高线.
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放以来,由于各阶段发展重心不同,某市的需求结构经历了消费投资交替主导、投资消费双轮驱动到消费主导的变化.到2007年,某市消费率超过投资率,标志着某市经济增长由投资消费双轮驱动向消费趋于主导过渡.下图是某市1978—2017年投资率与消费率统计图.根据统计图回答:________年,某市消费率与投资率相同;从2000年以后,某市消费率逐年上升的时间段是________.
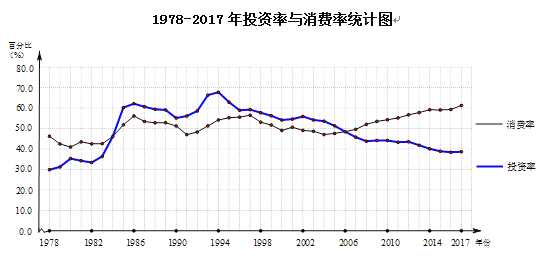
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上,王老师让同学们对给定的正方形ABCD,如图.建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是( )

A. 甲、乙、丙B. 乙、丙、丁C. 甲、丙D. 甲、乙、丙、丁
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
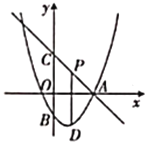
(1)求抛物线的解析式.
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求出
下方的抛物线上运动时,求出![]() 长度的最大值.
长度的最大值.
(3)当以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形时,求此时
为顶点的三角形是等腰三角形时,求此时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习了矩形后,数学活动小组开展了探究活动.如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,先以
上,先以![]() 为折痕将
为折痕将![]() 点往右折,如图2所示,再过点
点往右折,如图2所示,再过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示.
,如图3所示.
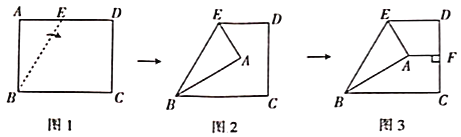
(1)在图3中,若![]() ,则
,则![]() 的度数为______,
的度数为______,![]() 的长度为______.
的长度为______.
(2)在(1)的条件下,求![]() 的长.
的长.
(3)在图3中,若![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目: 来源: 题型:
【题目】教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力,要增强学生的创新精神和综合素质.王老师想尝试改变教学方法,将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中,引导同学们解决菱形中的一个问题时,采用了以下过程(请解决王老师提出的问题):
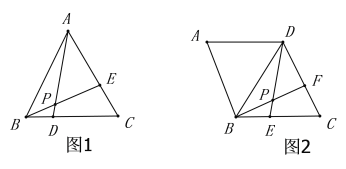
先出示问题(1):如图1,在等边三角形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,如果
上一点,如果![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,求
,求![]() 的度数.
的度数.
通过学习,王老师请同学们说说自己的收获.小明说发现一个结论:在这个等边三角形![]() 中,只要满足
中,只要满足![]() ,则
,则![]() 的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形
的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,
上一点,![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,如果
,如果![]() ,
,![]() ,求出菱形的边长.
,求出菱形的边长.
问题(3):通过以上的学习请写出你得到的启示(一条即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】某游乐场试营业期间,每天运营成本为1000元.经统计发现,每天售出的门票张数![]() (张)与门票售价
(张)与门票售价![]() (元/张)之间满足一次函数
(元/张)之间满足一次函数![]() ,设游乐场每天的利润为
,设游乐场每天的利润为![]() (元).(利润=票房收入-运营成本)
(元).(利润=票房收入-运营成本)
(1)试求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)游乐场将门票售价定为多少元/张时,每天获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com