
科目: 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
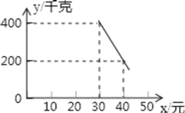
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图的菱形网格图中,每个小菱形的边长均为![]() 个单位,且每个小菱形内角中的锐角为60°.
个单位,且每个小菱形内角中的锐角为60°.
(1)直接写出![]() 的三个顶点
的三个顶点![]() 的坐标;
的坐标;
(2)在图中作出![]() 以点
以点![]() 为旋转中心,沿顺时针方向旋转60°后的图形
为旋转中心,沿顺时针方向旋转60°后的图形![]() ;
;
(3)根据(2),请直接写出线段![]() 扫过的面积.
扫过的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知菱形![]() 的边长为
的边长为![]() ,
,![]() =120°,对角线
=120°,对角线![]() 相交于点
相交于点![]() ,以点
,以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴,建立如图所示的直角坐标系,以
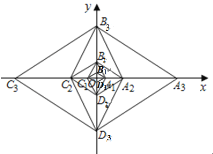
轴,建立如图所示的直角坐标系,以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() 菱形
菱形![]() ,…,按此规律继续做下去,设菱形
,…,按此规律继续做下去,设菱形![]() 的面积为
的面积为![]() ,菱形
,菱形![]() 的面积为
的面积为![]() ,…,菱形
,…,菱形![]() 的面积为
的面积为![]() ,则
,则![]() _____.
_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c为常数a≠0)与x轴,y轴分别交于A,B,C三点,已知A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点点D出发沿线段DB向终点B运动.
(1)直接写出抛物线解析式和顶点D的坐标;
(2)过点E作EF⊥y轴于点F,交抛物线对称轴左侧的部分于点G,交直线BC于点H,过点H作HP⊥x轴于点P,连接PF,求当线段PF最短时G点的坐标;
(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,点E的速度为每秒![]() 个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.
个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.

查看答案和解析>>
科目: 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目: 来源: 题型:
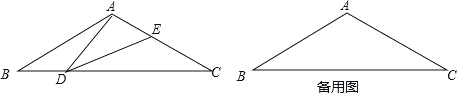
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com