
科目: 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
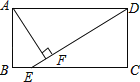
A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有点
轴上有点![]() ,连接
,连接![]() .
.
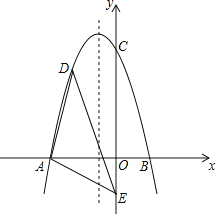
(1)求二次函数的解析式;
(2)若点![]() 为抛物线在x轴负半轴上方的一个动点,设点
为抛物线在x轴负半轴上方的一个动点,设点![]() 的横坐标为
的横坐标为![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有
为等腰三角形?若存在,请直接写出所有![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
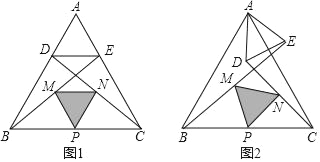
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想:图1中,△PMN的形状是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请直接写出△PMN的周长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案所示图形是顶点在原点的抛物线的部分,方案二所示的图形是射线, 设推销员销售产品的数量为![]() (件),付给推销员的月报酬为
(件),付给推销员的月报酬为![]() (元),
(元),
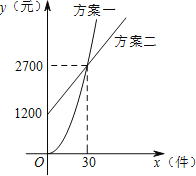
(1)请直接写出两种方案中![]() 关于
关于![]() 的函数关系式:方案一: ,方案二: ;
的函数关系式:方案一: ,方案二: ;
(2)当销售量达到多少件时,两种方案的月报酬差额将达到![]() 元?
元?
(3)若公司决定改进“方案二”:基本工资![]() 元,每销售件产品再增加报酬
元,每销售件产品再增加报酬![]() 元,当推销员销售量达到
元,当推销员销售量达到![]() 件时,方案二的月报酬不低于方案一的月报酬,求
件时,方案二的月报酬不低于方案一的月报酬,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知![]() 的半径为 4,
的半径为 4,![]() 是圆的直径,点
是圆的直径,点![]() 是
是![]() 的切线
的切线![]() 上的一个动点,连接
上的一个动点,连接![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 平行于
平行于![]() ,连接
,连接![]() .
.

(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
(3)当![]() ___________时,四边形
___________时,四边形![]() 为正方形.
为正方形.
查看答案和解析>>
科目: 来源: 题型:
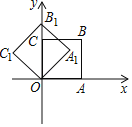
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目: 来源: 题型:
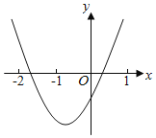
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
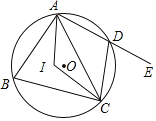
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目: 来源: 题型:
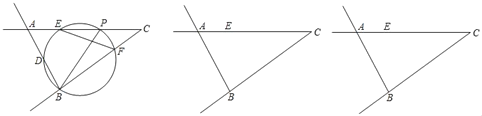
【题目】如图,在锐角△ABC中,BC=10,AC=11,△ABC的面积为33,点P是射线CA上一动点,以BP为直径作圆交线段AC于点E,交射线BA于点D,交射线CB于点F.
(1)当点P在线段AC上时,若点E为![]() 中点,求BP的长.
中点,求BP的长.
(2)连结EF,若△CEF为等腰三角形,求所有满足条件的BP值.
(3)将DE绕点D顺时针旋转90°,当点E的对应点E'恰好落在BC上时,记△DBE'的面积为S1,△DPE的面积S2,则![]() 的值为 .(直接写出答案即可)
的值为 .(直接写出答案即可)
查看答案和解析>>
科目: 来源: 题型:
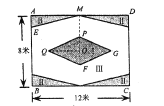
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com