
科目: 来源: 题型:
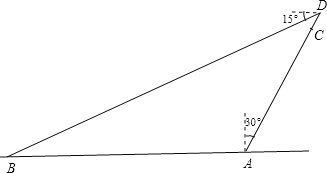
【题目】如图,在小山的东侧![]() 处有一一热气球,以每分钟28米的速度沿着与垂直方向夹角为30°的方向飞行,半小时后到达
处有一一热气球,以每分钟28米的速度沿着与垂直方向夹角为30°的方向飞行,半小时后到达![]() 处,这时气球上的人发现,在
处,这时气球上的人发现,在![]() 处的正西方向有一处着火点
处的正西方向有一处着火点![]() ,5分钟后,在
,5分钟后,在![]() 处测得着火点
处测得着火点![]() 的俯角是15°,求热气球升空点
的俯角是15°,求热气球升空点![]() 与着火点
与着火点![]() 的距离.(结果保留根号,参考数据:
的距离.(结果保留根号,参考数据: ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
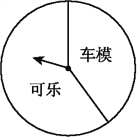
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
科目: 来源: 题型:
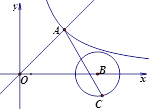
【题目】如图,一次函数![]() =
=![]() 与反比例函数
与反比例函数![]() =
=![]() (
(![]() >0)的图像在第一象限交于点A,点C在以B(7,0)为圆心,2为半径的⊙B上,已知AC长的最大值为
>0)的图像在第一象限交于点A,点C在以B(7,0)为圆心,2为半径的⊙B上,已知AC长的最大值为![]() ,则该反比例函数的函数表达式为__________________________.
,则该反比例函数的函数表达式为__________________________.
查看答案和解析>>
科目: 来源: 题型:
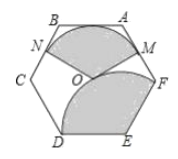
【题目】如图,点![]() 为正六边形
为正六边形![]() 的中心,点
的中心,点![]() 为
为![]() 中点,以点
中点,以点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧得到扇形
的长为半径画弧得到扇形![]() ,点
,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧得到扇形
的长为半径画弧得到扇形![]() ,把扇形
,把扇形![]() 的两条半径
的两条半径![]() 重合,围成圆锥,将此圆锥的底面半径记为
重合,围成圆锥,将此圆锥的底面半径记为![]() ;将扇形
;将扇形![]() 以同样方法围成的圆锥的底面半径记为
以同样方法围成的圆锥的底面半径记为![]() ,则
,则![]() =______.
=______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是弧
是弧![]() 的中点,弦
的中点,弦![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的外心;④
的外心;④![]()
![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.②③④C.①③④D.①②③④
查看答案和解析>>
科目: 来源: 题型:
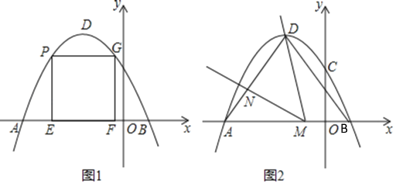
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0).
x2+bx+c经过点A(﹣5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A、D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G,过点G作GF⊥x轴于点F,当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD、BD,点M在线段AB上(不与A、B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
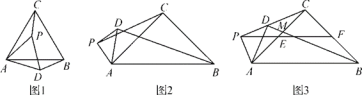
【题目】在△ABC中,CA=CB,∠ACB=α.点P 是平面内不与点A,C 重合的任意一点,连接AP,将线段AP 绕点P 逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)猜想观察:如图1,当α=60°时,![]() 的值是________,直线BD与直线CP相交所成的较小角的度数是________.
的值是________,直线BD与直线CP相交所成的较小角的度数是________.
(2)类比探究:如图2,当α=90°时,请写出![]() 的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由.
的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题:如图3,当α=90°时,若点 E,F 分别是 CA,CB 的中点,点 P 在FE的延长线上,P,D,C三点在同一直线上,AC与BD相交于点M,DM=2-![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】一家蔬菜公司计划到某绿色蔬菜基地收购A,B两种蔬菜共140吨,预计两种蔬菜销售后获利的情况如下表所示:
销售品种 | A种蔬菜 | B种蔬菜 |
每吨获利(元) | 1200 | 1000 |
其中A种蔬菜的5%,B种蔬菜的3%须运往C市场销售,但C市场的销售总量不超过5.8吨.设销售利润为W元(不计损耗),购进A种蔬菜x吨.
(1)求W与x之间的函数关系式;
(2)将这140吨蔬菜全部销售完,最多可获得多少利润?
(3)由于受市场因素影响,公司进货时调查发现,A种蔬菜每吨可多获利100元,B种蔬菜每吨可多获利m(200<m<400)元,但B种蔬菜销售数量不超过90吨.公司设计了一种获利最大的进货方案,销售完后可获利179000元,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和![]() 所围成的弓形的面积.
所围成的弓形的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com