
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.调查全校建档立卡户学生的人数,宜采用抽样调查
B.随机抽取某班7名学生的数学成绩:105,102,105,113,116,105,119,则数据的中位数和众数都是105
C.通过对甲、乙两组学生数学成绩的跟踪调查,整理得知两组数据的方差分别为:![]() =0.123,
=0.123,![]() =0.362,则乙组数据比甲组数据稳定
=0.362,则乙组数据比甲组数据稳定
D.必然事件发生的概率为1,随机事件发生的概率为0.5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() (﹣1,0)、
(﹣1,0)、![]() (3,0),与
(3,0),与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 为线段
为线段![]() 上的动点(不与
上的动点(不与![]() 、
、![]() 重合),过点
重合),过点![]() 垂直于
垂直于![]() 轴的直线与抛物线及线段
轴的直线与抛物线及线段![]() 分别交于点
分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() =2,连接
=2,连接![]() 、
、![]() .
.
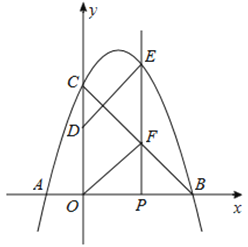
(1)求抛物线的解析式;
(2)当四边形![]() 是平行四边形时,求点
是平行四边形时,求点![]() 的坐标;
的坐标;
(3)过点![]() 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形![]() 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系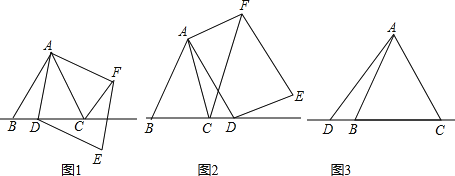
查看答案和解析>>
科目: 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
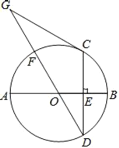
(1)判断CG与圆O的关系,并说明理由;
(2)若CD=6,求线段GF的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.

(1)画出△ABC绕点C按顺时针方向旋转90°的△A′B′C,并直接写出点A在旋转过程中所经过的路径长(结果保留![]() );
);
(2)在(1)的条件下,利用尺规作图画出△A′B′C的外接圆⊙P.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
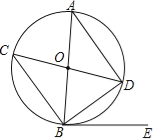
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=(x-1)2+n,当x=3时,y=2.
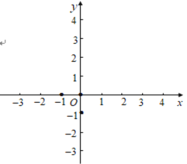
(1)求抛物线的解析式,并在平面直角坐标系中画出该函数的图象;
(2)过点D(0,2)作x轴的平行线交抛物线于E,F两点,求EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)圆中最长的弦是______.
(2)如图,AB是⊙O的弦,AB=8,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长度的最大值是_____.
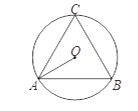
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
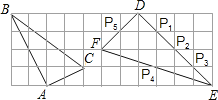
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:不写作法与证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com