
科目: 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
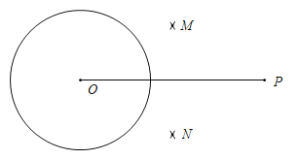
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合)过点
重合)过点![]() 分別作
分別作![]() 和
和![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() .
.

(1)关于矩形![]() 面积的探究:
面积的探究:
①点![]() 在何处时,矩形
在何处时,矩形![]() 的面积为1?写出计算过程;
的面积为1?写出计算过程;
②是否存在一点![]() ,能使矩形
,能使矩形![]() 的面积为
的面积为![]() ?说说你的理由.
?说说你的理由.
(2)设点![]() 的坐标是
的坐标是![]() ,
,![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,尝试完成下列问题:
,尝试完成下列问题:
①建立![]() 与
与![]() 的关系式,并类比一次函数猜想
的关系式,并类比一次函数猜想![]() 是
是![]() 的什么函数,能否对此类函数下一个描述性的定义,其中包含它的一般形式;
的什么函数,能否对此类函数下一个描述性的定义,其中包含它的一般形式;
②我们知道代数式![]() 有最小值9,试问当
有最小值9,试问当![]() 在何处时
在何处时![]() 有最小值,请把你的理由.
有最小值,请把你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个小风筝与一个大风等形状完全相同,它们的形状如图所示,其中对角线AC⊥BD.已知它们的对应边之比为1:3,小风筝两条对角线的长分別为12cm和14cm.

(1)小风筝的面积是多少?
(2)如果在大风筝内装设一个连接对角顶点的十字交叉形的支撑架,那么至少需用多长的材料?(不记损耗)
(3)大风筝要用彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为38.5°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高及大楼与塔之间的距离BC的长.
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80).

查看答案和解析>>
科目: 来源: 题型:
【题目】小颖、小明、小亮在解方程![]() 时,解法各不相同,请你回答下列问题:
时,解法各不相同,请你回答下列问题:
(1)简要分析一下三位同学的解法是否正确.如果正确,他运用了哪种解一元二次方程的方法;如果错误,错误的原因是什么?你是否从中体会到解一元二次方程的数学思想是什么?
(2)请你选择一种你熟练的方法尝试解一元二次方程![]() .
.
由方程 因此 所以这个数是0或3 | 方程
|
即 或 所以这个数是0或3. |
查看答案和解析>>
科目: 来源: 题型:
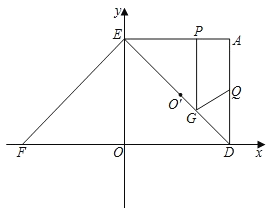
【题目】如图,等腰直角△OEF在坐标系中,有E(0,2),F(﹣2,0),将直角△OEF绕点E逆时针旋转90°得到△ADE,且A在第一象限内,抛物线y=ax2+bx+c经过点A,E.且2a+3b+5=0.
(1)求抛物线的解析式.
(2)过ED的中点O'作O'B⊥OE于B,O'C⊥OD于C,求证:OBO'C为正方形.
(3)如果点P由E开始沿EA边以每秒2厘米的速度向点A移动,同时点Q由点A沿AD边以每秒1厘米的速度向点D移动,当点P移动到点A时,P,Q两点同时停止,且过P作GP⊥AE,交DE于点G,设移动的开始后为t秒.
①若S=PQ2(厘米),试写出S与t之间的函数关系式,并写出t的取值范围?
②当S取最小时,在抛物线上是否存在点R,使得以P,A,Q,R为顶点的四边形是平行四边形?如果存在,求出R的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
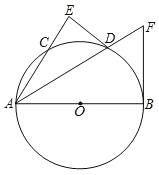
【题目】如图,AB是直经,D是![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
(1)求证:DE是⊙O的切线.
(2)试探究AE,AD,AB三者之间的等量关系.
(3)若DE=3,⊙O的半径为5,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com