
科目: 来源: 题型:
【题目】“双十一购物狂欢节”来临之际,某超市拟举办购物促销活动,从分店调动了20名店员参与总店活动,其中男店员8人,女店员12人.

(1)若从这20人中随机选取一人作为宣传人员,求选到女店员的概率;
(2)分店的某活动中需要甲、乙两店员中选一人参与,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加,请用树状图或列表法分别求出甲、乙两人参加这项活动的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,一枚质地均匀的骰子,骰子有六个面并分别标有数字1,2,3,4,5,6.如图2,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 7个圈,相邻两个圈间距相等.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的数字是几,就从圈
7个圈,相邻两个圈间距相等.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的数字是几,就从圈![]() 开始向前连续跳几个间距.如:从圈
开始向前连续跳几个间距.如:从圈![]() 起跳,第一次掷得3,就连续跳3个间距,跳到圈
起跳,第一次掷得3,就连续跳3个间距,跳到圈![]() ;若第二次掷得3,就从
;若第二次掷得3,就从![]() 开始连续跳3个间距,跳到圈
开始连续跳3个间距,跳到圈![]() ;若第二次掷得4,就从圈
;若第二次掷得4,就从圈![]() 开始连续跳4个间距,跳到圈
开始连续跳4个间距,跳到圈![]() 后返回到圈
后返回到圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.
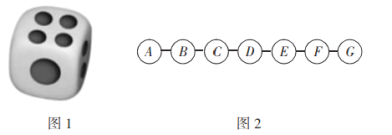
(1)小明随机掷一次骰子,求跳到圈![]() 的概率
的概率![]() ;
;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后跳到圈![]() 的概率
的概率![]() ,并指出他与小明跳到圈
,并指出他与小明跳到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目: 来源: 题型:
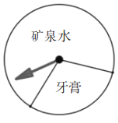
【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物50元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在某一区域就可以获得该区域相对应的奖品.若恰巧落在两区域交界线上,则重新转动转盘.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“矿泉水”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
假如你去转动该转盘一次,你获得牙膏的概率约是______.(用小数表示,结果保留一位小数)
查看答案和解析>>
科目: 来源: 题型:
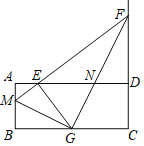
【题目】在矩形ABCD中,AB=4,AD=10,E是AD的一点,且AE=2,M是AB上一点,射线ME交CD的延长线于点F,EG⊥ME交BC于点G,连接MG,FG,FG交AD于点N.
(1)当点M为AB中点时,则DF= ,FG= .(直接写出答案)
(2)在整个运动过程中,![]() 的值是否会变化,若不变,求出它的值;若变化,请说明理由.
的值是否会变化,若不变,求出它的值;若变化,请说明理由.
(3)若△EGN为等腰三角形时,请求出所有满足条件的AM的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅(购买的数量不超过8吨),包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(单位:吨)之间的函数关系如图所示.
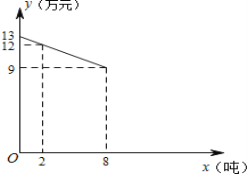
(1)求y与x的函数表达式?
(2)当销售数量为多少时,该公司经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)
(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是![]()
①当该公司销售杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?
②该公司销售杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
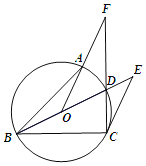
【题目】已知,如图,BD为⊙O的直径,点A、C在⊙O上并位于BD的两侧,∠ABC=45°,连结CD、OA并延长交于点F,过点C作⊙O的切线交BD延长线于点E.
(1)求证:∠F=∠ECF;
(2)当DF=6,tan∠EBC=![]() ,求AF的值.
,求AF的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(﹣3,0),(0,﹣3).
(1)求抛物线的表达式.
(2)已知点(m,k)和点(n,k)在此抛物线上,其中m≠n,请判断关于t的方程t2+mt+n=0是否有实数根,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
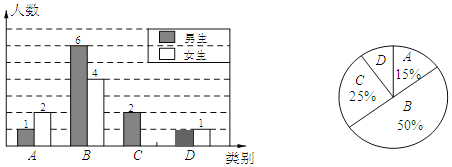
【题目】李老师为了解某校学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.绘制成如下统计图.
(1)李老师一共调查了多少名同学?并将下面条形统计图补充完整.
(2)若该校有1000名学生,则数学课前预习“很好”和“较好”总共约多少人?
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,求出所选两位同学恰好是一位男同学和一位女同学的概率.(要求列表或树状图)
查看答案和解析>>
科目: 来源: 题型:
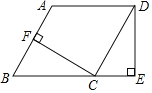
【题目】如图,在ABCD中,CF⊥AB于点F,过点D作DE⊥BC的延长线于点E,且CF=DE.
(1)求证:△BFC≌△CED;
(2)若∠B=60°,AF=5,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
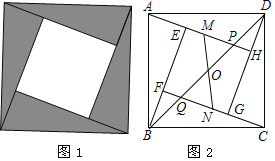
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com