
科目: 来源: 题型:
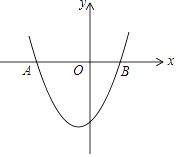
【题目】如图,已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧).
(1)求A、B的坐标;
(2)利用函数图象,写出y<0时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
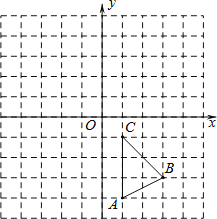
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣4)、B(3,﹣3)、C(1,﹣1)(每个小方格都是边长为一个单位长度的正方形).
(1)请画出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2B2C2.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013+…+i2019的值为( )
A.0B.1C.﹣1D.i
查看答案和解析>>
科目: 来源: 题型:
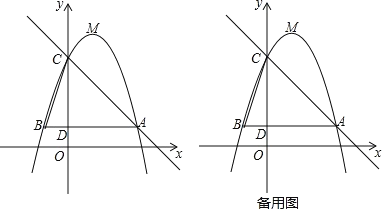
【题目】如图,已知二次函数![]() (b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移![]() 个单位,使平移后得到的二次函数图象的顶点与△ABC的外心重合,求
个单位,使平移后得到的二次函数图象的顶点与△ABC的外心重合,求![]() 的取值;
的取值;
(3)点P是坐标平面内的一点,使得△ACB与△MCP,且CM的对应边为AC,请写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目: 来源: 题型:
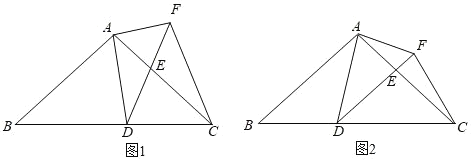
【题目】如图1,在△ABC中,AB=AC=10,BC=16,点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如图1,抛物线![]() 与x轴交于A,B两点,点P在该抛物线上(P点与A. B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边
与x轴交于A,B两点,点P在该抛物线上(P点与A. B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边![]() 倍,则称点P为抛物线
倍,则称点P为抛物线![]() 的“好”点.
的“好”点.
(1)命题:P(0,3)是抛物线![]() 的“好”点.该命题是_____( 真或假)命题.
的“好”点.该命题是_____( 真或假)命题.
(2)如图2,已知抛物线C:![]() 与
与![]() 轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.
轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.
(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目: 来源: 题型:
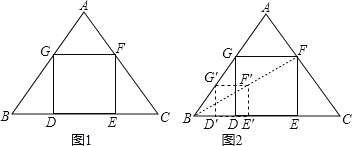
【题目】如图,△ABC是一块等边三角形的废铁片,其中AB=AC=10![]() ,BC=12
,BC=12![]() .利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
.利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
(1)小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.请你帮小聪求出正方形的边长.
(2)小明想:不求正方形的边长也能画出正方形.具体作法是:
①在AB边上任取一点G′,如图2作正方形G′D′E′F′;
②连接BF′并延长交AC于点F;
③过点F作FE∥F′E′交BC于点E,FG∥F′G′交AB于点G,GD∥G′D′交BC于点D,则四边形DEFG即为所求的正方形.你认为小明的作法正确吗?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件.经过调查发现,这种商品的销售单价每提高1元,其销售量相应减少20件.设这种商品的销售单提高![]() 元.
元.
(1)现每天的销售量为 件,现每件的利润为 元.
(2)求这种商品的销售单价提高多少元时,才能使每天所获利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】最近诸暨城市形象宣传片《西施故里好美诸暨》正式发布,此篇历时6个月拍摄,从不同角度向世界介绍了诸暨,现有一个不透明的口袋装有分别标有汉字“好”、“美”、“诸”、“暨”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字“美”的概率是多少.
(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图或列表的方法,求出甲取出的两个球上的汉字恰能组成“诸暨”的概率P.
查看答案和解析>>
科目: 来源: 题型:
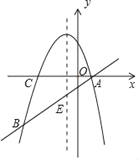
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com