【题目】某水果店销售一批水果，平均每天可售出，每千克盈利元，经调查发现，每千克降价元，商店平均每天可多售出水果，则商店平均每天的最高利润为______________ 元

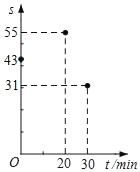
A. 8min B. 13min C. 20min D. 25min

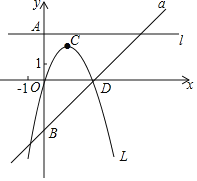
（1）若AB=8，求b的值，并求此时L的对称轴与a的交点坐标；

（2）当点C在l下方时，求点C与l距离的最大值；

（3）设x0≠0，点（x0，y1），（x0，y2），（x0，y3）分别在l，a和L上，且y3是y1，y2的平均数，求点（x0，0）与点D间的距离；

（4）在L和a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b=2019和b=2019.5时“美点”的个数．

【题目】已知二次函数图象的顶点在原点，对称轴为轴．一次函数的图象与二次函数的图象交于两点（在的左侧），且点坐标为．平行于轴的直线过点．

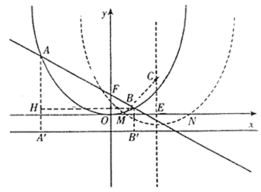
（1）求一次函数与二次函数的解析式；

（2）判断以线段AB为直径的圆与直线的位置关系，并给出证明；

（3）把二次函数的图象向右平移 2 个单位，再向下平移 t 个单位（t＞0），二次函数的图象与x 轴交于 M，N 两点，一次函数图象交y 轴于 F 点．当 t 为何值时，过 F，M，N 三点的圆的面积最小？最小面积是多少？

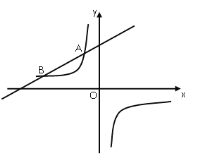
【题目】如图，一次函数（为常数，且）的图像与反比例函数的图像交于，两点.

（1）求一次函数的表达式；

（2）若将直线向下平移个单位长度后与反比例函数的图像有且只有一个公共点，求的值.

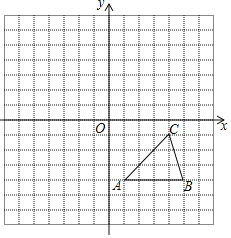
（1）把△ABC向上平移5个单位后得到对应的△A1B1C1，画出△A1B1C1；

（2）画出与△ABC关于原点O对称的△A2B2C2；

（3）△A1B1C1与△A2B2C2关于某个点对称，则这个点的坐标为　 　．

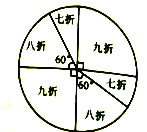
（1）某顾客正好消费220元，他转一次转盘，他获得九折、八折、七折优惠的概率分别是多少？

（2）某顾客消费中获得了转动一次转盘的机会，实际付费168元，请问他消费所购物品的原价应为多少元.

【题目】如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，与x轴的一个交点在（﹣3，0）和（﹣4，0）之间，其部分图象如图所示则下列结论：①4a﹣b＝0；②c＜0；③c＞3a；④4a﹣2b＞at2+bt（t为实数）；⑤点（﹣，y1），（﹣，y2），（）是该抛物线上的点，则y2＜y1＜y3，其中，正确结论的个数是（　　）

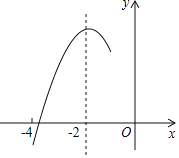
A. 1B. 2C. 3D. 4

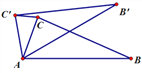
A. 70° B. 35° C. 40° D. 90°

青年最喜爱的新四大发明人数统计表

青年最喜爱的新四大发明人数条形统计图

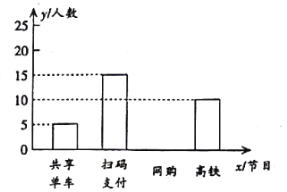
（1）计算的值 ；

（2）请补全条形统计图；

（3）在被调查喜爱“共享单车”青年中，小明一周内使用共享单车的次数分别为：1，3，5，12，，若整数是这组数据的中位数，直接写出该组数据的平均数.