
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)甲队队员身高的平均数为 厘米,乙队队员身高的平均数为 厘米;
(2)你认为哪支仪仗队更为整齐?简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两名战士在相同条件下各射击10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7 乙:6,7,7,6,7,8,7,9,8,5
(1)分别求出两组数据的方差和标准差;
(2)根据计算结果,评价一下两名战士的射击情况.
查看答案和解析>>
科目: 来源: 题型:
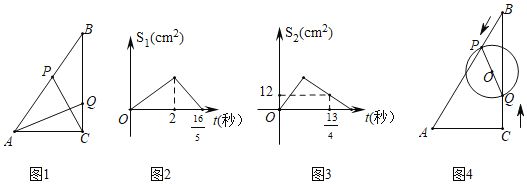
【题目】如图(1),在Rt△ABC中,∠ACB=90°,AC=6cm,动点P从点B出发,沿折线B→A→C路线匀速运动到C停止,动点Q从点C出发,沿折线C→B→A路线匀速运动到A停止,如点P、Q同时出发运动t秒后,如图(2)是△BPC的面积S1(cm2)与t(秒)的函数关系图象,图(3)是△AQC的面积S2(cm2)与t(秒)的函数关系图象:
(1)点P运动速度为 cm/秒;Q运动的速度 cm/秒;
(2)连接PQ,当t为何值时,PQ∥BC;
(3)如图(4)当运动t(0≤t≤2)秒时,是否存在这样的时刻,使以PQ为直径的⊙O与Rt△ABC的一条边相切,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),在△ABC中,如果正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,那么我们称这样的正方形为“三角形内接正方形”小波同学按数学家波利亚在《怎样解题》中的方法进行操作:如图(2),任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结BN′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN,小波把线段BN称为“波利亚线”,请帮助小波解决下列问题:
(1)四边形PQMN是否是△ABC的内接正方形,请证明你的结论;
(2)若△ABC为等边三角形,边长BC=6,求△ABC内接正方形的边长;
(3)如图(3),若在“波利亚线”BN上截取NE=NM,连结EQ,EM.当![]() 时,猜想∠QEM的度数,并说明你的理由.
时,猜想∠QEM的度数,并说明你的理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
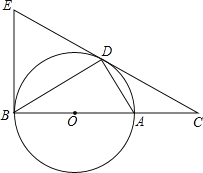
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
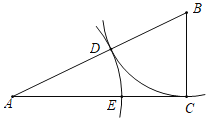
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC的长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,设BC=a,AC=b.
(1)请你判断:线段AD的长度是方程x2+2ax﹣b2=0的一个根吗?说明理由;
(2)若线段AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】用一根长22cm的铁丝,
(1)能否围成面积是30cm2的矩形?如果能,求出矩形的边长,如果不能说明理由;
(2)能否围成面积是32cm2的矩形?如果能,求出矩形的边长,如果不能说明理由;
(3)请探索能围成的矩形面积的最大值是多少 cm2?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若m是整数,且方程有两个不相等的整数根,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com