
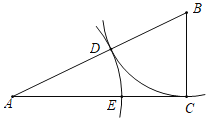
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC的长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,设BC=a,AC=b.
(1)请你判断:线段AD的长度是方程x2+2ax﹣b2=0的一个根吗?说明理由;
(2)若线段AD=EC,求![]() 的值.
的值.
【答案】(1)线段AD的长度是方程x2+2ax﹣b2=0的一个根,理由详见解析;(2)![]() .
.
【解析】
(1)方程变形即可得到![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,由
,由![]() ,即可得到结论;
,即可得到结论;
(2)由题意得,![]() ,根据勾股定理列出
,根据勾股定理列出![]() ,整理得到
,整理得到![]() ,即可求得
,即可求得![]() .
.
解:(1)∵在△ABC中,∠ACB=90°,
∴AB2=AC2+BC2,
∵BC=a,AC=b.
∴AB2=a2+b2,
方程x2+2ax﹣b2=0变形为:x2+2ax+a2=a2+b2,
∴(x+a)2=AB2,
∵BD=BC=a,
∴(x+BD)2=AB2,
∵(AD+BD)2=AB2,
∴线段AD的长度是方程x2+2ax﹣b2=0的一个根;
(2)∵AD=EC,
∴AC=2AD=2AE=b,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
整理得![]() ,
,
![]()
![]() .
.


科目:初中数学 来源: 题型:
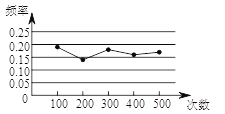
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
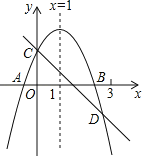
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
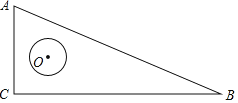
【题目】如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为![]() ,则△ABC的周长为_____.
,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)甲队队员身高的平均数为 厘米,乙队队员身高的平均数为 厘米;
(2)你认为哪支仪仗队更为整齐?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为
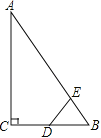
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
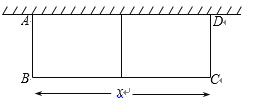
【题目】如图,利用一面墙(墙的长度为15 m),用篱笆围成一个矩形花园ABCD,中间再用一道篱笆隔成两个小矩形,共用去篱笆42 m.设平行于墙的一边BC长为x m,花园的面积为S m2.
(1)求S与x之间的函数解析式;
(2)问花园面积可以达到120平方米吗?如果能,花园的长和宽各是多少?如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com