【题目】如图，在中，，将绕点顺时针旋转一定角度后得到，连接,过点作交于点，若，且，则的长为__________．

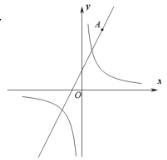
【题目】如图，在平面直角坐标系内，为坐标原点，点为直线上一动点，过作轴，交轴于点（点在原点右侧），交双曲线于点，且，则当存在时，其面积为__________．

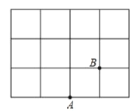
【题目】如图，在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点，任意三个格点组成的三角形面积如果不小于1则称为“离心三角形”，而如果面积恰好等于1则称为“环绕三角形”．是网格图形中已知的两个格点，点是另一个格点，且满足是“离心三角形”，则是“环绕三角形”的概率是__________．

【题目】已知，甲、乙两人分别从两地出发，相向而行，已知甲先出发4分钟后，乙才出发，他们两人在之间的地相遇，相遇后，甲立即返回地，乙继续向地前行．甲到达地时停止行走，乙到达地是也停止行走，在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程（米）与甲出发的时间（分钟）之间的关系如图所示，则下列结论错误的是（ ）

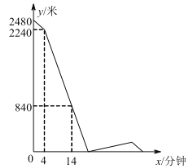
A.两地相距2480米B.甲的速度是60米/分钟，乙的速度是80米/分钟

C.乙出发17分钟后，两人在地相遇D.乙到达地时，甲与地相距的路程是300米．

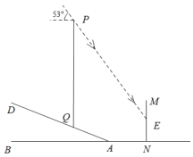
【题目】重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号，保证广大师生网络授课、听课的质量，临时在坡度为的山坡上加装了信号塔（如图所示），信号塔底端到坡底的距离为3.9米．同时为了提醒市民，在距离斜坡底4.4米的水平地面上立了一块警示牌．当太阳光线与水平线成53°角时，测得信号塔落在警示牌上的影子长为3米，则信号塔的高约为（tan53°≈1.3）（ ）.

A.10.4B.11.9C.11.4D.13.4

【题目】最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽，赵爽创制了一幅“勾股圆方图”，用数形结合的方法，给出了勾股定理的详细证明．在这幅“勾股圆方图”中，以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的小正方形组成的．设直角三角形的两直角边长为，且满足，若小正方形的面积为11，则大正方形的面积为（ ）

A.15B.17C.30D.34

【题目】如图，矩形中，，，点在上，连接点在直线上，交于点．

（1）求证：是等腰三角形；

（2）求证：；

（3）当为中点时，求的长．

（1）求y与x的函数关系式，并写出自变量x的取值范围；

（2）顾客一次性购买多少件时，该网店从中获利最多？

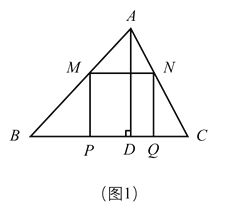
【题目】如图在锐角中，，高，两动点、分别在、上滑动（不包含端点），且，以为边长向下作正方形，设，正方形与公共部分的面积为．

（1）如图（1），当正方形的边恰好落在边上时，求的值．

（2）如图（2），当落外部时，求出与的函数关系式（写出的取值范围）并求出为何值时最大，最大是多少？

(1)求抛物线y＝x2﹣2x+2与x轴的“和谐值”；

(2)求抛物线y＝x2﹣2x+2与直线y＝x﹣1的“和谐值”．