
科目: 来源: 题型:
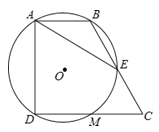
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:
①DM=CM;②弧AB=弧EM;③⊙O的直径为2;④AE=AD.
其中正确的结论有______(填序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )

A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图a,当点H与点F重合时,求BE的长;
(2)如图b,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出它的定义域;
(3)连接AC,当△FHE与△AEC相似时,求线段DN的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.
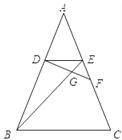
求证:(1)△DEF∽△BDE;(2)DGDF=DBEF.
查看答案和解析>>
科目: 来源: 题型:
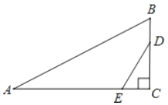
【题目】在Rt△ABC中,∠C=90°,AC=8,BC=6,点D、E分别在BC、AC上,且BD=CE,设点C关于DE的对称点为F,若DF∥AB,则BD的长为__________.
查看答案和解析>>
科目: 来源: 题型:
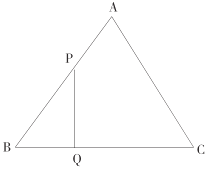
【题目】如图,已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别沿
两点出发,分别沿![]() 、
、![]() 方向匀速移动,它们的移动速度都是
方向匀速移动,它们的移动速度都是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 、
、![]() 两点停止运动,设点
两点停止运动,设点![]() 的运动时间的
的运动时间的![]() 秒,解答下列问题.
秒,解答下列问题.
(1)![]() 时,求
时,求![]() 的面积;
的面积;
(2)若![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(3)用![]() 表示
表示![]() 的面积并判断
的面积并判断![]() 能否成立,若能成立,求
能否成立,若能成立,求![]() 的值,若不能成立,说明理由.
的值,若不能成立,说明理由.
查看答案和解析>>
科目: 来源: 题型:
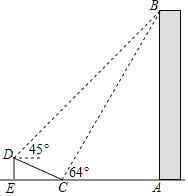
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目: 来源: 题型:
【题目】王某承包了甲、乙两片荒山,各栽了100棵杨梅树,现已全部挂果,为了分析收成情况,他分别从两山上各采摘了4棵树上的全部杨梅,每棵树的产量如折线统计图.
(1)分别计算甲、乙两山样本的平均数,并估计出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?

查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的点M和图形W1,W2给出如下定义:点P为图形W1上一点,点Q为图形W2上一点,当点M是线段PQ的中点时,称点M是图形W1,W2的“中立点”.如果点P(x1,y1),Q(x2,y2),那么“中立点”M的坐标为(![]() ,
,![]() ).
).
已知,点A(-3,0),B(0,4),C(4,0).
(1)连接BC,在点D(![]() ,0),E(0,1),F(0,
,0),E(0,1),F(0,![]() )中,可以成为点A和线段BC的“中立点”的是______;
)中,可以成为点A和线段BC的“中立点”的是______;
(2)已知点G(3,0),⊙G的半径为2,如果直线y=-x+1存在点K可以成为点A和⊙G的“中立点”,求点K的坐标;
(3)以点C为圆心,半径为2作圆,点N为直线y=2x+4上的一点,如果存在点N,使得y轴上的一点可以成为点N与⊙C的“中立点”,直接写出点N的横坐标的取值范围.
查看答案和解析>>
科目: 来源: 题型:
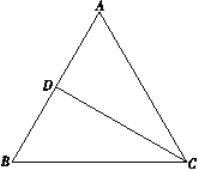
【题目】如图1,在等边三角形ABC中,CD为中线,点Q在线段CD上运动,将线段QA绕点Q顺时针旋转,使得点A的对应点E落在射线BC上,连接BQ,设∠DAQ=α
(0°<α<60°且α≠30°).
(1)当0°<α<30°时,
①在图1中依题意画出图形,并求∠BQE(用含α的式子表示);
②探究线段CE,AC,CQ之间的数量关系,并加以证明;
(2)当30°<α<60°时,直接写出线段CE,AC,CQ之间的数量关系.

![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com