
科目: 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目: 来源: 题型:
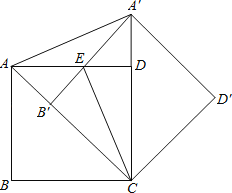
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整.例题:求一元二次方程![]() 的两个解.
的两个解.
(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解.解方程:![]() ;
;
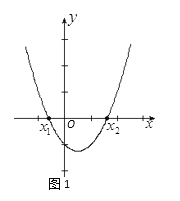
(2)解法二:利用二次函数图象与坐标轴的交点求解,如图1所示,把方程![]() 的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
(3)解法三:利用两个函数图象的交点求解.
①把方程![]() 的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;
的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;
②画出这两个函数的图象,用x1,x2在x轴上标出方程的解.
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目: 来源: 题型:
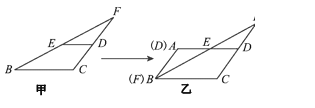
【题目】如图甲,已知ED是△FBC的中位线,沿线段ED将△FED剪下后拼接在图乙中△BEA的位置.
(1)从△FED到△BEA的图形变换,可以认为是(填平移或轴对称或旋转)变换;
(2)试判断图乙中四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
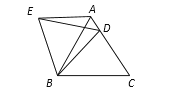
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=8,BD=6.则下列四个结论:①∠AEB=∠BDC;②AE∥BC;③△BDE是等边三角形;④△ADE的周长是14.其中正确的结论是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的部分对应值如下表:
的部分对应值如下表:
x | … | -3 | -2 | 0 | 3 | 5 | … |
y | … | 7 | 0 | -8 | -5 | 7 | … |
则以下四个结论:①图象的开口向上;②函数的最小值为-8;③方程![]() 的两根分别-2,4;④若y<-5,则-1<x<3.其中正确结论的个数是( )
的两根分别-2,4;④若y<-5,则-1<x<3.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=mx2﹣4mx+2m+1与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=2.

(1)求抛物线的解析式;
(2)E是抛物线上一点,∠EAB=2∠OCA,求点E的坐标;
(3)设抛物线的顶点为D,动点P从点B出发,沿抛物线向上运动,连接PD,过点P做PQ⊥PD,交抛物线的对称轴于点Q,以QD为对角线作矩形PQMD,当点P运动至点(5,t)时,求线段DM扫过的图形面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com