
科目: 来源: 题型:
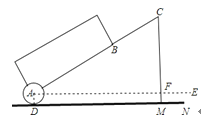
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

①把![]() 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的![]() ,画出
,画出![]() ,并写出
,并写出![]() 的坐标;
的坐标;
②以原点![]() 为对称中心,画出
为对称中心,画出![]() 与关于原点
与关于原点![]() 对称的
对称的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
③以原点O为旋转中心,画出把![]() 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,直线
轴交于点C,直线![]() 经过A、C两点.
经过A、C两点.
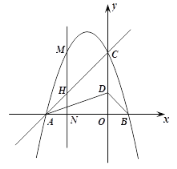
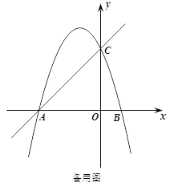
(1)求抛物线的解析式;
(2)点N是![]() 轴上的动点,过点N作
轴上的动点,过点N作![]() 轴的垂线,交抛物线与点M,交直线AC于点H.
轴的垂线,交抛物线与点M,交直线AC于点H.
①点D在线段OC上,连结AD、BD,当![]() 时,求
时,求![]() 的最小值;
的最小值;
②当![]() 时,将直线AD绕点A旋转
时,将直线AD绕点A旋转![]() ,使直线AD与
,使直线AD与![]() 轴交于点P,请直接写出点P的坐标.
轴交于点P,请直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在△ABC中,![]() ,D、E分别是边AB、BC上的动点,且
,D、E分别是边AB、BC上的动点,且![]() ,连结AD、AE,点M、N、P分别是CD、AE、AC的中点,设
,连结AD、AE,点M、N、P分别是CD、AE、AC的中点,设![]() .
.
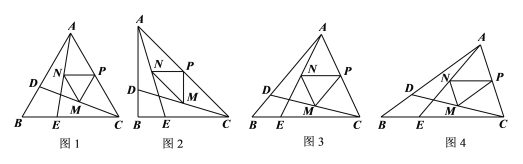
(1)观察猜想
①在求![]() 的值时,小明运用从特殊到一般的方法,先令
的值时,小明运用从特殊到一般的方法,先令![]() ,解题思路如下:
,解题思路如下:
如图1,先由![]() ,得到
,得到![]() ,再由中位线的性质得到
,再由中位线的性质得到![]() ,
,
![]() ,进而得出△PMN为等边三角形,∴
,进而得出△PMN为等边三角形,∴![]() .
.
②如图2,当![]() ,仿照小明的思路求
,仿照小明的思路求![]() 的值;
的值;
(2)探究证明
如图3,试猜想![]() 的值是否与
的值是否与![]() 的度数有关,若有关,请用含
的度数有关,若有关,请用含![]() 的式子表示出
的式子表示出![]() ,若无关,请说明理由;
,若无关,请说明理由;
(3)拓展应用
如图4,![]() ,点D、E分别是射线AB、CB上的动点,且
,点D、E分别是射线AB、CB上的动点,且![]() ,点M、N、P分别是线段CD、AE、AC的中点,当
,点M、N、P分别是线段CD、AE、AC的中点,当![]() 时,请直接写出MN的长.
时,请直接写出MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着第27届信阳茶文化节发布会、固始西九华山第三届郁金香风情文化节等系列活动的成功举办,越来越多的游客想要到信阳游玩小明所在的公司想在五一黄金周期间组织员工去信阳游玩,咨询了甲、乙两家旅行社,两家旅行社分别推出优惠方案(未推出优惠方案前两家旅行社的收费标准相同).甲:购买一张团体票,然后个人票打六折优惠;乙:不购买团体票,当团体人数超过一定数量后超过部分的个人票打折优惠,优惠期间,公司的员工人数为x(人),在甲旅行社所需总费用为![]() (元),在乙旅行社所需总费用为
(元),在乙旅行社所需总费用为![]() (元).
(元).![]() 、
、![]() 与x之间的函数关系如图所示.
与x之间的函数关系如图所示.
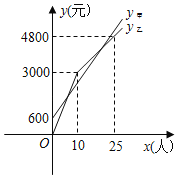
(1)甲旅行社团体票是______元,乙旅行社团体人数超过一定数量后,个人票打______折;
(2)求![]() 、
、![]() 关于x的函数表达式;
关于x的函数表达式;
(3)请说明小明所在的公司选择哪个旅行社出游更划算.
查看答案和解析>>
科目: 来源: 题型:
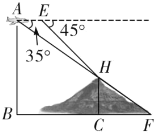
【题目】如图所示,为了测量某矿山CH的高度,科考组在距离矿山一段距离的B点乘坐直升机垂直上升2000米至A点,在A点,在A点观察H点的俯角为![]() ,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为
,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为![]() ,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据:
,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】随着2019年全国两会的隆重召开,中学生对时事新闻的关注空前高涨,某校为了解中学生对时事新闻的关注情况,组织全校九年级学生开展“时事新闻大比拼”比赛,随机抽取九年级的25名学生的成绩(满分为100分)整理统计如下:收集数据 25名学生的成绩(满分为100分)统计如下(单位:分)
90 ,74 ,88 ,65 ,98 ,75 , 81 ,44 ,85 ,70 ,55 , 80 , 95 ,88 ,72 ,87 , 60 ,56 ,76 ,66 ,78 ,72 ,82 ,63 ,100
整理数据:按如下分组整理样本数据并补全表格:
成绩 | 90≤ | 75≤ | 60≤ |
|
人数 | 10 | 8 |
分析数据 补充完成下面的统计分析表:
平均数 | 中位数 | 方差 |
76 | 190. 88 |
得出结论:
(1)若全校九年级有1000名学生,请估计全校九年级有多少学生成绩达到90分及以上;
(2)若八年级的平均数为76分,中位数为80分,方差为102. 5,请你分别从平均数、中位数和方差三个方面做出评价,你认为哪个年级的成绩较好?
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,其中有这样一道名题:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几步及之?”意思是说:走路快的人走100步的时候,走路慢的才走了60步,走路慢的人先走100步,然后走路快的人去追赶,问走路快的人要走多少部才能追上?若设走路快的人要走x步才能追上走路慢的人,此时走路慢的人又走了y步,根据题意可列方程组为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
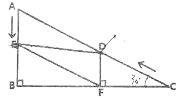
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() 秒
秒![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)![]() ______.(用含
______.(用含![]() 的代数式表示)
的代数式表示)
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由.
值;如果不能,请说明理由.
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形![]() 的边长为6,
的边长为6,![]() 是边
是边![]() 上的一点,
上的一点,![]() 绕点
绕点![]() 逆时针旋转后得到
逆时针旋转后得到![]() .
.![]() 三点在同一直线上.
三点在同一直线上.
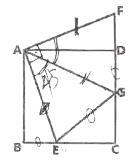
(1)求四边形![]() 的面积.
的面积.
(2)如果点![]() 在边
在边![]() 上,且
上,且![]() ,试判断
,试判断![]() 之间有什么样的数量关系?并说明理由.
之间有什么样的数量关系?并说明理由.
(3)在(2)的条件下,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com