
科目: 来源: 题型:
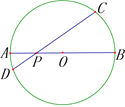
【题目】已知:AB是⊙O的直径,P是OA上一点,过点P作⊙O的非直径的弦CD.
(1)若PA=2,PB=10,∠CPB=30°,求CD长;
(2)求证:PCPD=PAPB;
(3)设⊙O的直径为8,若PC、PD是方程![]() ,求m的范围.
,求m的范围.
查看答案和解析>>
科目: 来源: 题型:
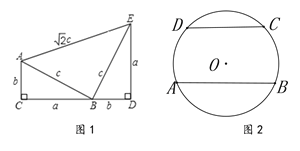
【题目】如图1,四边形ACDE是美国第二十任总统伽菲尔德验证勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE=![]() ,这时我们把关于x的形如
,这时我们把关于x的形如![]() 的一元二次方程称为“勾系一元二次方程”.
的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)判断方程![]() 是否是 “勾系一元二次方程”;并说明理由.
是否是 “勾系一元二次方程”;并说明理由.
(2)求证:关于![]() 的“勾系一元二次方程”
的“勾系一元二次方程” ![]() 必有实数根;
必有实数根;
(3)如图2,已知AB、CD是半径为5的⊙O的两条平行弦,AB=2a,CD=2b,a≠b,关于x的方程![]() 是“勾系一元二次方程”,求∠BAC的度数
是“勾系一元二次方程”,求∠BAC的度数
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点A(1,0),已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.
(1)当抛物线经过点A时.
①求顶点P的坐标;
②设直线l:y=3x+1与抛物线交于B、C两点,抛物线上的点M的横坐标为n(﹣1≤n≤3),过点M作x轴的垂线,与直线l交于点Q,若MQ=d,当d随n的增大而减少时,求n的取值范围.
(2)无论m取何值,该抛物线都经过定点H,当∠AHP=45°时,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,将此矩形绕点B顺时针方向旋转θ(0<θ<180°)得到矩形A1BC1D1,直线BA1、C1D1分别与直线CD相交于点E、F.
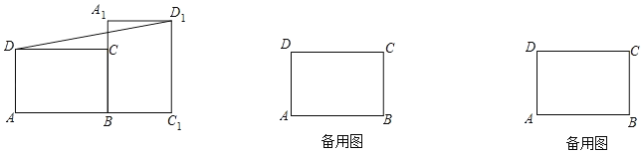
(1)若此矩形绕点B顺时针方向旋转90°,求DD1的长;
(2)在旋转过程中,点D、A1、D1三点共线时,求△BCE的面积;
(3)在矩形ABCD旋转的过程中,是否存在某个位置使得以B、E、F、D1为顶点的四边形为平行四边形?若存在,求出CF的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们可以通过下列步骤估计方程x2﹣2x﹣2=0方程的根所在的范围.
第一步:画出函数y=x2﹣2x﹣2=0的图象,发现函数图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,﹣1之间.
第二步:因为当x=0时,y=﹣2<0,当x=﹣1时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x1所在的范围是﹣1<x1<0
第三步:通过取0和﹣1的平均数缩小x1所在的范围:
取x=![]() ,因为当x=
,因为当x=![]() 对,y<0.又因为当x=﹣1时,y>0,所以
对,y<0.又因为当x=﹣1时,y>0,所以![]()
(1)请仿照第二步,通过运算验证方程x2﹣2x﹣2=0的另一个根x2所在的范围是2<x2<3
(2)在2<x2<3的基础上,重复应用第三步中取平均数的方法,将x2所在的范围缩小至a<x2<b,使得![]() .
.
查看答案和解析>>
科目: 来源: 题型:
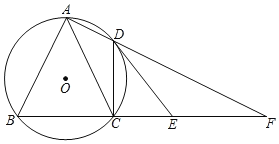
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AB=AC,CE=10,EF=14,求CD.
查看答案和解析>>
科目: 来源: 题型:
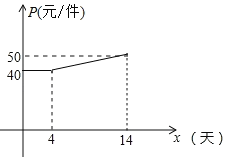
【题目】我市高新区某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的售价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:![]() .
.
(1)工人甲第几天生产的产品数量为60件?
(2)设第x天生产的产品成本为P元/件,P与x的函数关系图象如图,工人甲第x天创造的利润为W元,求W与x的函数关系式,第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
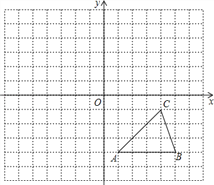
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com