
科目: 来源: 题型:
【题目】涌泉镇是中国无核蜜桔之乡,已知某蜜桔种植大户冯大爷的蜜桔成本为2元/千克,如果在未来90天蜜桔的销售单价p(元/千克)与时间t(天)之间的函数关系式为p=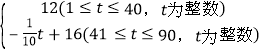 ,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
时间t/天 | 1 | 10 | 20 | 40 | 70 | 90 |
日销售量y/千克 | 105 | 150 | 200 | 300 | 450 | 550 |
(1)求y与t之间的函数表达式;
(2)在未来90天的销售中,预测哪一天的日销售利润最大?最大日销售利润为多少元?
(3)在实际销售的后50天中,冯大爷决定每销售1千克蜜桔就捐赠n元利润(n<5)给留守儿童作为助学金,销售过程中冯大爷发现,恰好从第51天开始,和前一天相比,扣除捐赠后的日销售利润逐日减少,请求出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,其中图象与
的部分图象如图所示,其中图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.
![]() 求此二次函数的解析式;
求此二次函数的解析式;
![]() 将此二次函数的解析式写成
将此二次函数的解析式写成![]() 的形式,并直接写出顶点坐标以及它与
的形式,并直接写出顶点坐标以及它与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
![]() 利用以上信息解答下列问题:若关于
利用以上信息解答下列问题:若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 为实数)在
为实数)在![]() 的范围内有解,则
的范围内有解,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目: 来源: 题型:
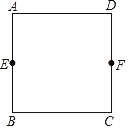
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目: 来源: 题型:
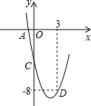
【题目】为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.
(1)小明一共调查了多少户家庭?
(2)所调查家庭5月份用水量的中位数、众数、平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(﹣3,0),与y轴交点为B,且与正比例函数y=![]() x的图象交于点C(m,4)
x的图象交于点C(m,4)
(1)求m的值及一次函数y=kx+b的表达式;
(2)观察函数图象,直接写出关于x的不等式![]() x≤kx+b的解集;
x≤kx+b的解集;
(3)若P是y轴上一点,且△PBC的面积是8,直接写出点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形纸片ABCD边长为6,点E,F分别是AB,CD的中点,点G,H分别在AD,AB上,将纸片沿直线GH对折,当顶点A与线段EF的三等分点重合时,AH的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=12,G、H是线段AB的三等分点,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,![]() =
=![]() ,M,N分别是对角线AC,BE的中点,在点P从点G运动到点H的过程中,MN的长度的取值范围是()
,M,N分别是对角线AC,BE的中点,在点P从点G运动到点H的过程中,MN的长度的取值范围是()
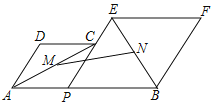
A.![]() ≤MN≤6B.
≤MN≤6B.![]() ≤MN≤
≤MN≤![]()
C.![]() ≤MN≤6D.
≤MN≤6D.![]() ≤MN≤
≤MN≤![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
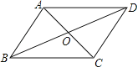
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
科目: 来源: 题型:
【题目】点![]() 为图形
为图形![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 直线
直线![]() 垂足为
垂足为![]() ,记
,记![]() 的长度为
的长度为![]() .
.
定义一:若![]() 存在最大值,则称其为“图形
存在最大值,则称其为“图形![]() 到直线
到直线![]() 的限距离”,记作
的限距离”,记作![]() ;
;
定义二:若![]() 存在最小值,则称其为“图形
存在最小值,则称其为“图形![]() 到直线
到直线![]() 的基距离”,记作
的基距离”,记作![]() ;
;
(1)已知直线![]() ,平面内反比例函数
,平面内反比例函数![]() 在第一象限内的图象记作
在第一象限内的图象记作![]() 则
则![]() .
.
(2)已知直线![]() ,点
,点![]() ,点
,点![]() 是
是![]() 轴上一个动点,
轴上一个动点,![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上,若
上,若![]() 求此时
求此时![]() 的取值范围,
的取值范围,
(3)已知直线![]() 恒过定点
恒过定点![]() ,点
,点![]() 恒在直线
恒在直线![]() 上,点
上,点![]() 是平面上一动点,记以点
是平面上一动点,记以点![]() 为顶点,原点为对角线交点的正方形为图形
为顶点,原点为对角线交点的正方形为图形![]()
![]() ,若请直接写出
,若请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com