
科目: 来源: 题型:
【题目】![]() 、
、![]() 为
为![]() 的切线,切点分别为点
的切线,切点分别为点![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
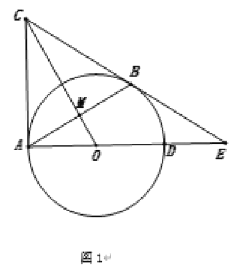
(1)如图1,求证:![]() ;
;
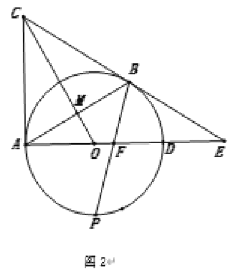
(2)如图2,点![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交AD于点
交AD于点![]() ,求证:
,求证:![]() ;
;
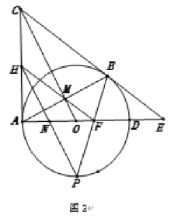
(3)如图3,在(2)的条件下:连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
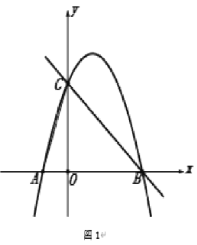
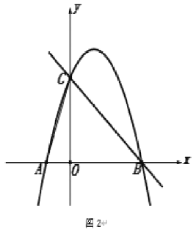
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)如图2,![]() 为第一象限内抛物线上一点,
为第一象限内抛物线上一点,![]() 的面积为3时,且
的面积为3时,且![]() ,求
,求![]() 点坐标;
点坐标;
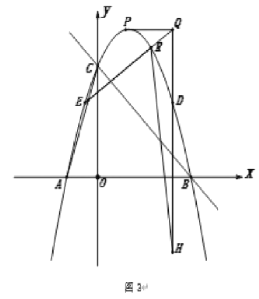
(3)如图3,在(2)的条件下,![]() 、
、![]() 为抛物线上的点,且两点关于抛物线对称轴对称,过
为抛物线上的点,且两点关于抛物线对称轴对称,过![]() 作
作![]() 轴垂线交过点
轴垂线交过点![]() 且平行于
且平行于![]() 轴的直线于
轴的直线于![]() ,
,![]() 交抛物线于
交抛物线于![]() ,延长
,延长![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,当线段
,当线段![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
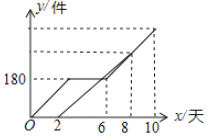
【题目】某快递公司甲、乙两名快递员7月上旬10天里派送快递,乙比甲晚工作一段时间,工作期间快递员甲因事停工3天,各自的工作效率一定,他们各自的工作量![]() (件)随工作时间
(件)随工作时间![]() (天)变化的图像如图所示.则有下列说法:①甲工人的工作效率为60件/天;②乙工人每天比甲工人少送10件;③甲工人一共送420件;④乙比甲少工作2天.其中正确的个数是( )
(天)变化的图像如图所示.则有下列说法:①甲工人的工作效率为60件/天;②乙工人每天比甲工人少送10件;③甲工人一共送420件;④乙比甲少工作2天.其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
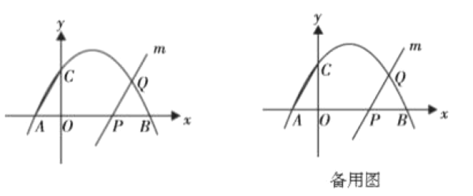
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是射线
是射线![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() ,与
,与![]() 轴右侧的抛物线交于点
轴右侧的抛物线交于点![]() .点
.点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒1个单位长度的速度向右运动,设点
以每秒1个单位长度的速度向右运动,设点![]() 运动的时间为t秒.请解答下列问题:
运动的时间为t秒.请解答下列问题:
(1)求直线AC的表达式与点![]() 的坐标;
的坐标;
(2)在点![]() 运动的过程中,若以点
运动的过程中,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求运动的时间
为顶点的四边形是平行四边形,求运动的时间![]() ;
;
(3)设点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
①点![]() 的坐标为 (用含
的坐标为 (用含![]() 的代数式表示,结果需化简);
的代数式表示,结果需化简);
②当点![]() 落在抛物线
落在抛物线![]() 的对称轴上且点
的对称轴上且点![]() 在线段
在线段![]() 上时,在平面内是否存在点F,使得以点
上时,在平面内是否存在点F,使得以点![]() ,
,![]() ,
,![]() ,F为顶点的四边形为菱形?若存在,请求出此时点F的坐标;若不存在,请说明理由.
,F为顶点的四边形为菱形?若存在,请求出此时点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
在数学活动课上,老师给出![]() ,
,![]() ,
,![]() .点
.点![]() 为
为![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上运动,将线段
上运动,将线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,连接
,连接![]() ,
,![]() .过点
.过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图1,
上,如图1,
①根据题意补全图1(不要求尺规作图);
②判断![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)若点![]() 为线段
为线段![]() 的延长线上一点,如图2,且
的延长线上一点,如图2,且![]() ,
,![]() ,补全图2,求
,补全图2,求![]() 的面积.
的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
古希腊几何学家海伦,在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中,给出了三角形面积的计算公式(海伦公式):如果一个三角形的三边长分别为![]() ,记
,记![]() ,那么三角形的面积是
,那么三角形的面积是![]() .
.
印度算术家波罗摩笈多和婆什迦罗还给出了四边形面积的计算公式:如果一个四边形的四边长分别为![]() ,记
,记![]() ,那么四边形的面积是
,那么四边形的面积是![]() (其中,
(其中,![]() 和
和![]() 表示四边形的一组对角的度数)
表示四边形的一组对角的度数)
根据上述信息解决下列问题:
(1)已知三角形的三边是4,6,8,则这个三角形的面积是
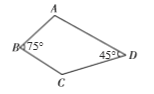
(2)小明的父亲是工程师,设计的某个零件的平面图是如图的四边形![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .求出这个零件平面图的面积.
.求出这个零件平面图的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取![]() 学校与
学校与![]() 学校的各20名学生的数学成绩(单位:分)进行
学校的各20名学生的数学成绩(单位:分)进行
| 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
| 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 1 | 1 | 0 | 0 | 3 | 7 | 8 |
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
| 81.85 | 88 | 91 | 268.43 |
| 81.95 | 86 | m | 115.25 |
得出结论:
![]() :若
:若![]() 学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
![]() :根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
:根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目: 来源: 题型:
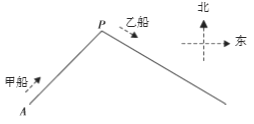
【题目】小岛![]() 在港口
在港口![]() 的南偏西45°方向,距离港口81海里处.甲船从
的南偏西45°方向,距离港口81海里处.甲船从![]() 出发,沿
出发,沿![]() 方向以6海里/时的速度驶向港口,乙船从港口
方向以6海里/时的速度驶向港口,乙船从港口![]() 出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
(1)出发后 小时两船与港口![]() 的距离相等;
的距离相等;
(2)出发几小时后乙船在甲船的正东方向?(结果精确到0.1小时,参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com