练习册

  • 练习册
  • 试题
    相关习题
     0  366081  366089  366095  366099  366105  366107  366111  366117  366119  366125  366131  366135  366137  366141  366147  366149  366155  366159  366161  366165  366167  366171  366173  366175  366176  366177  366179  366180  366181  366183  366185  366189  366191  366195  366197  366201  366207  366209  366215  366219  366221  366225  366231  366237  366239  366245  366249  366251  366257  366261  366267  366275  366461 

    科目： 来源： 题型：

    【题目】如果点P（2x＋6，x－4）在平面直角坐标系的第四象限内，那么x的取值范围在数轴上可表示为

    A. B. C. D.

    查看答案和解析>>

    科目： 来源： 题型：

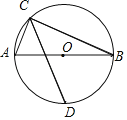
    【题目】如图，AB是⊙O的直径，点C是⊙O上一点（点C不与A，B重合），连接CA，CB．∠ACB的平分线CD与⊙O交于点D．

    （1）求∠ACD的度数；

    （2）探究CA，CB，CD三者之间的等量关系，并证明；

    （3）E为⊙O外一点，满足ED＝BD，AB＝5，AE＝3，若点P为AE中点，求PO的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知抛物线y＝x2+（1﹣2a）x﹣2a（a是常数）．

    （1）证明：该抛物线与x轴总有交点；

    （2）设该抛物线与x轴的一个交点为A（m，0），若2＜m≤5，求a的取值范围；

    （3）在（2）的条件下，若a为整数，将抛物线在x轴下方的部分沿x轴向上翻折，其余部分保持不变，得到一个新图象G，请你结合新图象，探究直线y＝kx+1（k为常数）与新图象G公共点个数的情况．

    查看答案和解析>>

    科目： 来源： 题型：

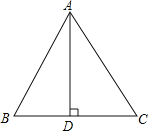
    【题目】如图，在等边△ABC中，AB＝6，AD是高．

    （1）尺规作图：作△ABC的外接圆⊙O（保留作图痕迹，不写作法）

    （2）在（1）所作的图中，求线段AD，BD与弧所围成的封闭图形的面积．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】为改善生态环境，建设美丽乡村，某村规划将一块长18米，宽10米的矩形场地建设成绿化广场，如图，内部修建三条宽相等的小路，其中一条路与广场的长平行，另两条路与广场的宽平行，其余区域种植绿化，使绿化区域的面积为广场总面积的80%．

    （1）求该广场绿化区域的面积；

    （2）求广场中间小路的宽．

    查看答案和解析>>

    科目： 来源： 题型：

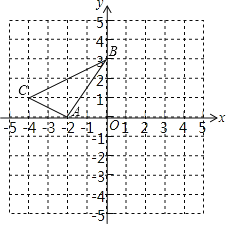
    【题目】如图，在平面直角坐标系xOy中，A（﹣2，0），B（0，3），C（﹣4，1）．以原点O为旋转中心，将△ABC顺时针旋转90°得到△A'B'C'，其中点A，B，C旋转后的对应点分别为点A'，B'，C'．

    （1）画出△A'B'C'，并写出点A'，B'，C'的坐标；

    （2）求经过点B'，B，A三点的抛物线对应的函数解析式．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】为了创建文明城市，增弘环保意识，某班随机抽取了8名学生（分别为A，B，C，D，E，F，G，H），进行垃圾分类投放检测，检测结果如下表，其中“√”表示投放正确，“×”表示投放错误，

    学生

    垃圾类别

    A

    B

    C

    D

    E

    F

    G

    H

    可回收物

    √

    ×

    ×

    √

    √

    ×

    √

    √

    其他垃圾

    ×

    √

    √

    √

    √

    ×

    √

    √

    餐厨垃圾

    √

    √

    √

    √

    √

    √

    √

    √

    有害垃圾

    ×

    √

    ×

    ×

    ×

    √

    ×

    √

    （1）检测结果中，有几名学生正确投放了至少三类垃圾？请列举出这几名学生．

    （2）为进一步了解学生垃圾分类的投放情况，从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈，求抽到学生A的概率．

    查看答案和解析>>

    科目： 来源： 题型：

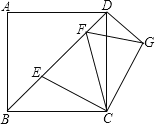
    【题目】如图，在正方形ABCD中，AB＝a，点E，F在对角线BD上，且∠ECF＝∠ABD，将△BCE绕点C旋转一定角度后，得到△DCG，连接FG．则下列结论：

    ①∠FCG＝∠CDG；

    ②△CEF的面积等于；

    ③FC平分∠BFG；

    ④BE2+DF2＝EF2；

    其中正确的结论是_____．（填写所有正确结论的序号）

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在下列函数图象上任取不同两点P（x1，y1），Q（x2，y2），一定能使（x2﹣x1）（y2﹣y1）＞0成立的是（　　）

    A.y＝﹣2x+1（x＜0）B.y＝﹣x2﹣2x+8（x＜0）

    C.y＝（x＞0）D.y＝2x2+x﹣6（x＞0）

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】下列抛物线中，其顶点在反比例函数y＝的图象上的是（　　）

    A.y＝（x﹣4）2+3B.y＝（x﹣4）2﹣3C.y＝（x+2）2+1D.y＝（x+2）2﹣1

    查看答案和解析>>

    同步练习册答案